[Grasshopper] Three ways to extract points where curves intersect

When using Grasshopper, there are times when you want to extract the intersection of curves lines.

In this issue, we will introduce three methods for extracting curve intersections.

As a conclusion, you can extract intersections by using “Curve | Curve,” “Curve | Self,” and “Multiple Curves.

Let’s look at them one by one.

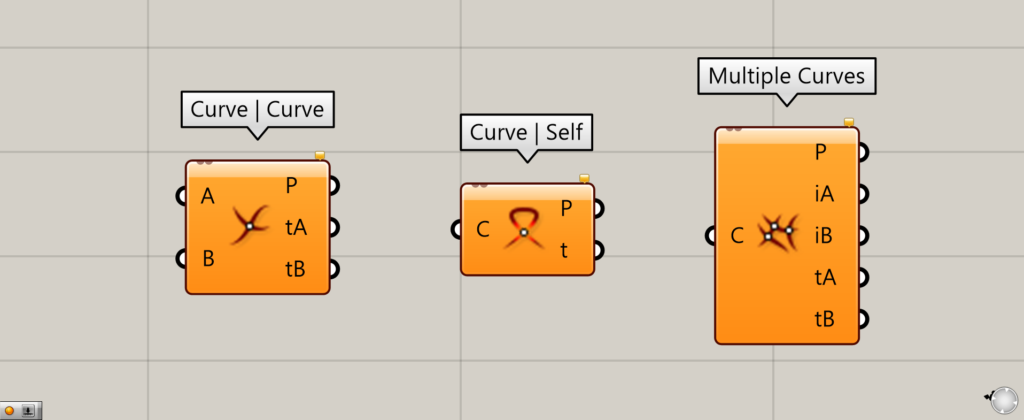
Curve | Curve

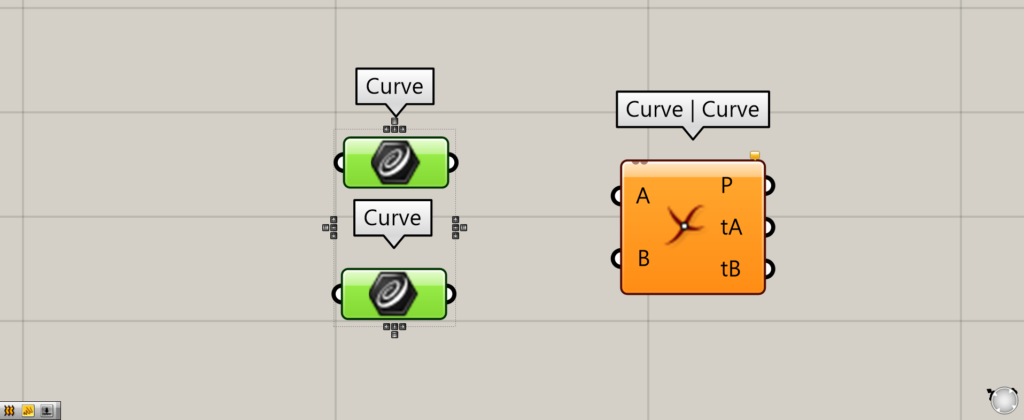
Components used: (1) Curve (2) Curve | Curve

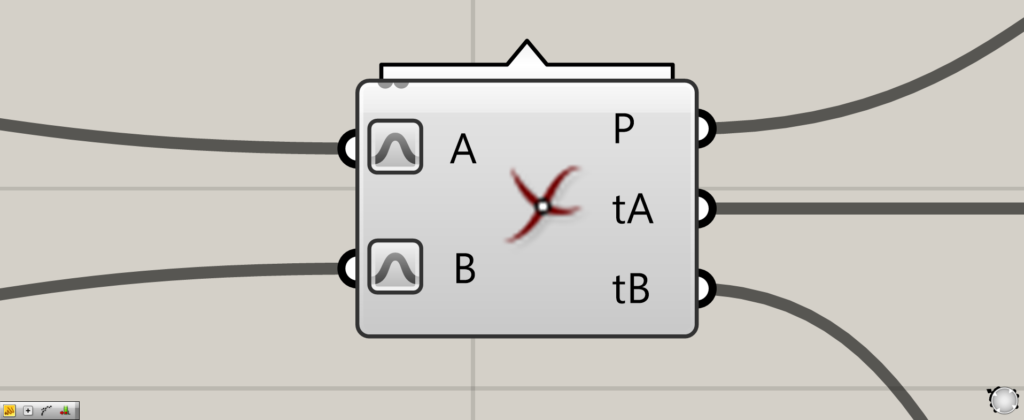
“Curve | Curve” can be used to extract the intersection of two curves.

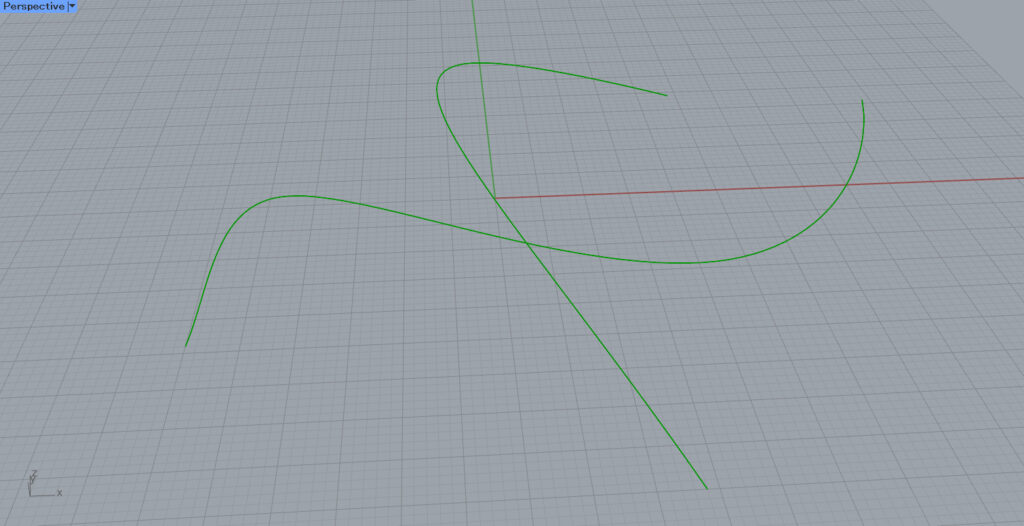
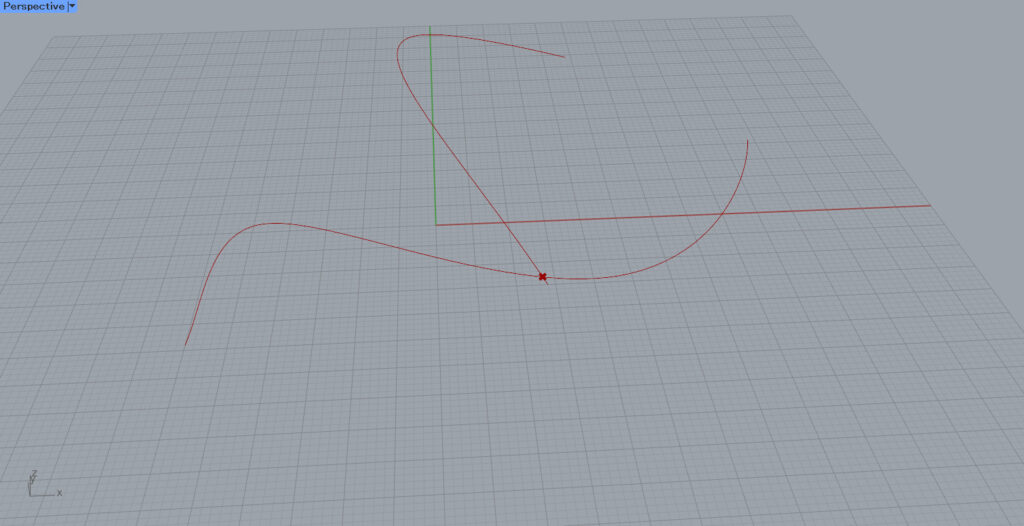
First, set each of the two intersecting lines in a Curve.

In this case, we prepared two curves as shown in the image above.

Then, connect the Curve to the Curve | Curve(A and B), respectively

The intersection of the two curves is then extracted.

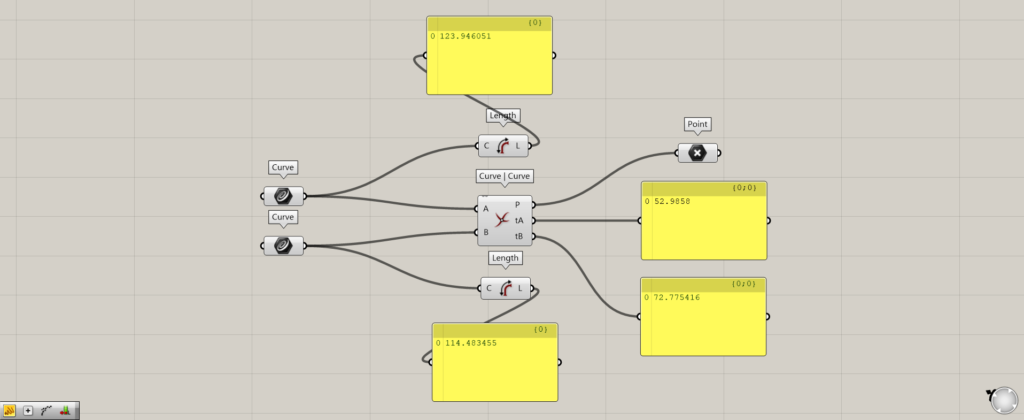
Components used: (1) Curve (2) Curve | Curve (3) Length (4) Point

Let’s look at the data output from Curve | Curve.

From the Curve | Curve(P), the point data of the intersection is extracted.

From the Curve | Curve(tA), it tells us where in the first curve data the intersection point is located.

Using Length, we can look at the length of the line.

We find that the length of the line is approximately 123.

If we look at tA, we see that it is approximately 52.

This means that the intersection is at about 52 of the first 123 length of the curve.

On the other hand, the Curve | Curve(tB) tells us where in the second curve data the intersection is located.

Reparameterize allows us to know the location of the intersection from 0~1.

Right-click on the Curve | Curve(A and B).

Then select Reparameterize.

Then, both terminals are now Reparameterized.

This time, for clarity, we moved the intersection point closer to the end of one of the curves.

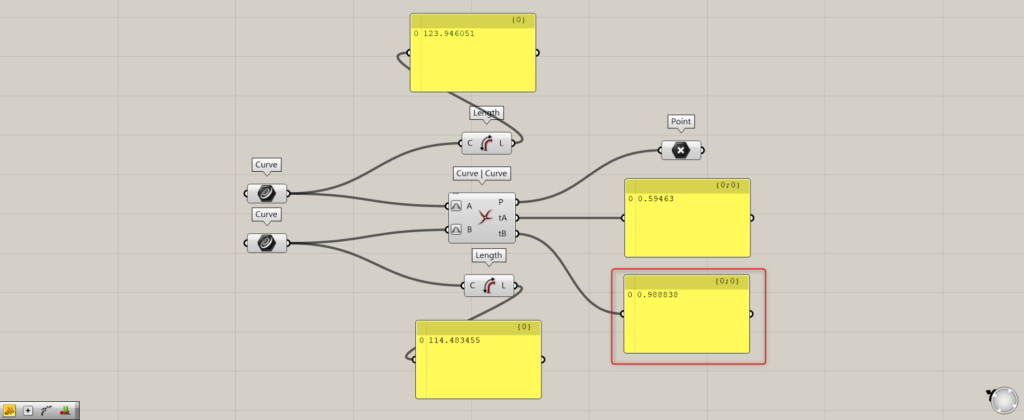
Then, from tA and tB, the values are now displayed as 0~1.

A 0 means that the intersection is at the beginning of the curve, while a 1 means that it is at the end of the curve.

Since we just moved one curve near the endpoint, tB is now about 0.98, which is very close to 1.

Curve | Self

Components used: (1) Curve (2) Curve | Self

Curve | Self can be used to extract the intersection of a single curve.

Set one intersecting curve, as shown in the image above, in Curve.

Then, connect the Curve to the Curve | Self(C).

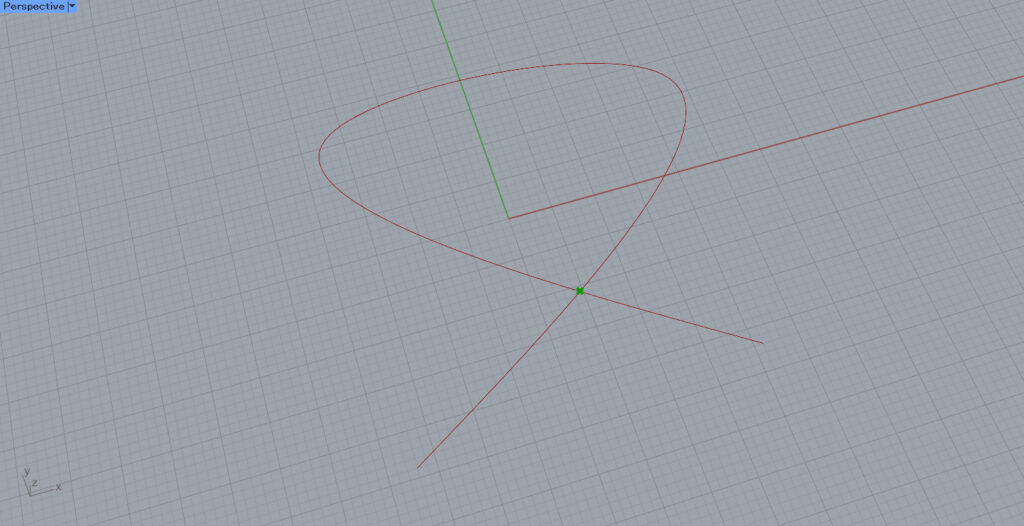
Then, the intersection of the curves is extracted as shown in the image above.

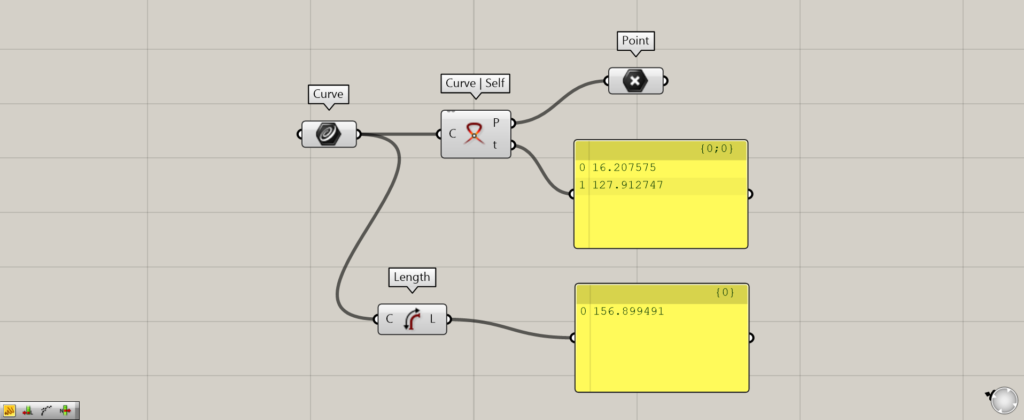
Components used: (1) Curve (2) Curve | Self (3) Length (4) Point

Let’s look at the data output from Curve | Self.

The Curve | Self(P) outputs the point data of the intersection.

The Curve | Self(t) tells us the position of the intersection point from the starting point of the curve.

In this case, the total length of the line is about 156.

Looking at the Curve | Self(t), the distance from the starting point to the intersection point is about 16.

In the other case, the intersection is located at about 127 of the curve.

Multiple Curves

Components used: (1) Curve (2) Multiple Curves

Multiple Curves can be used to extract the intersection of multiple curves.

In this case, we set multiple line data in Curve, as shown in the image above.

Then, connect the Curve to the Multiple Curves(C).

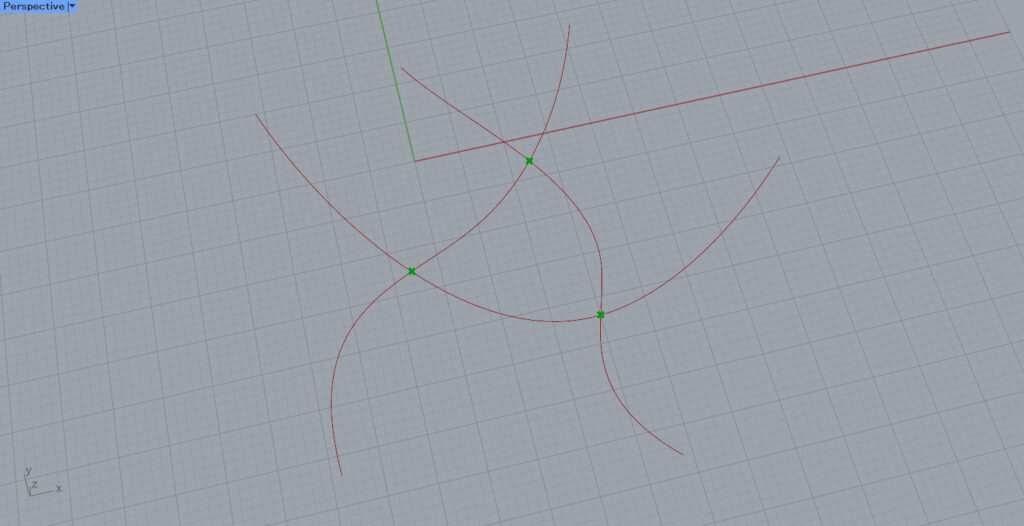
Then, the intersection points of multiple curves are extracted as shown in the image above.

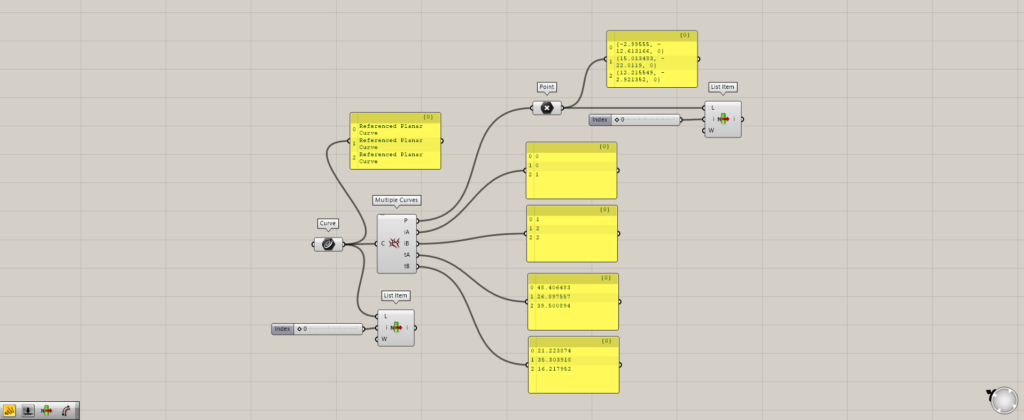
Components used: (1) Curve (2) Multiple Curves (3) Point (4) List Item

Let’s look at the data output from Multiple Curves.

The Multiple Curves(P) outputs the point data of the intersection.

The Multiple Curve( iA and iB) output the index numbers of the intersection points of each curve.

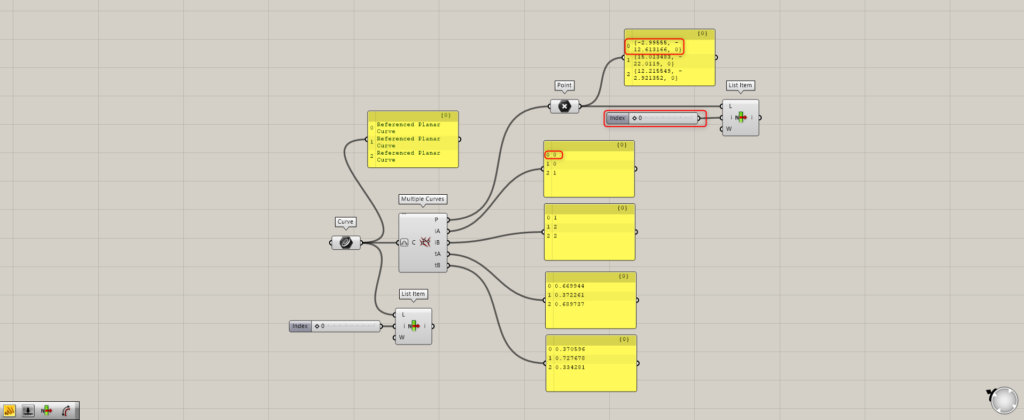
Using List Item, let’s first look at the point with Index number 0.

The first curve, iA, is labeled 0.

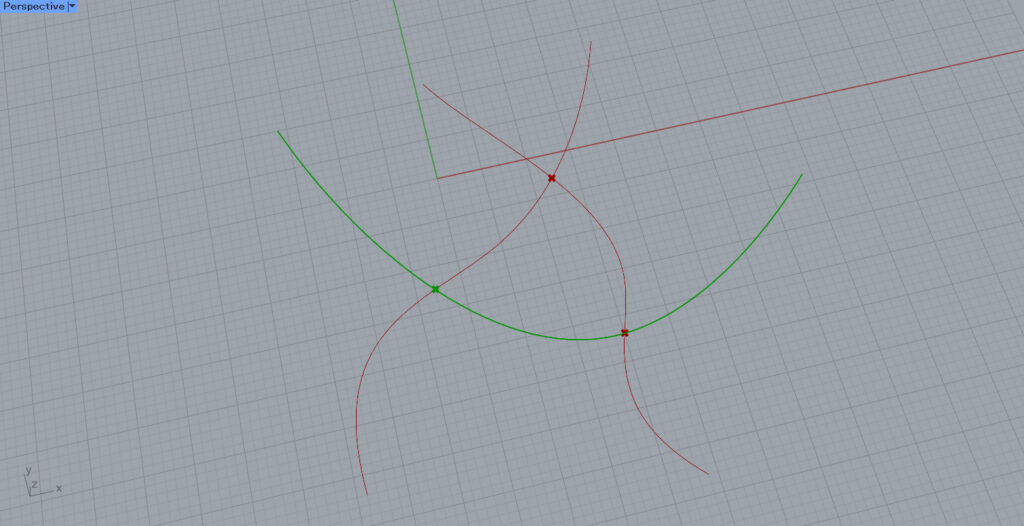
Then one intersection point on one curve is selected.

The Index number of this intersection is 0.

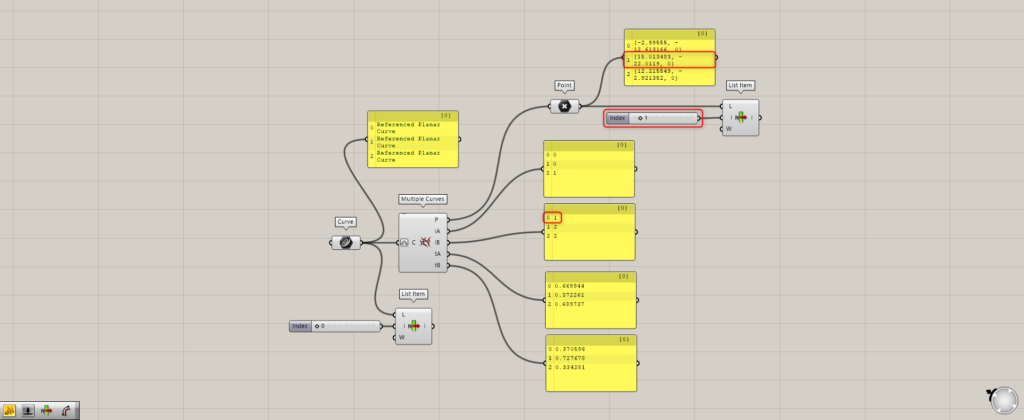
Next, let’s look at Multiple Curves(iB).

Then, in iB on the first curve, it is displayed as 1.

Let’s look at Index number 1 in the point data.

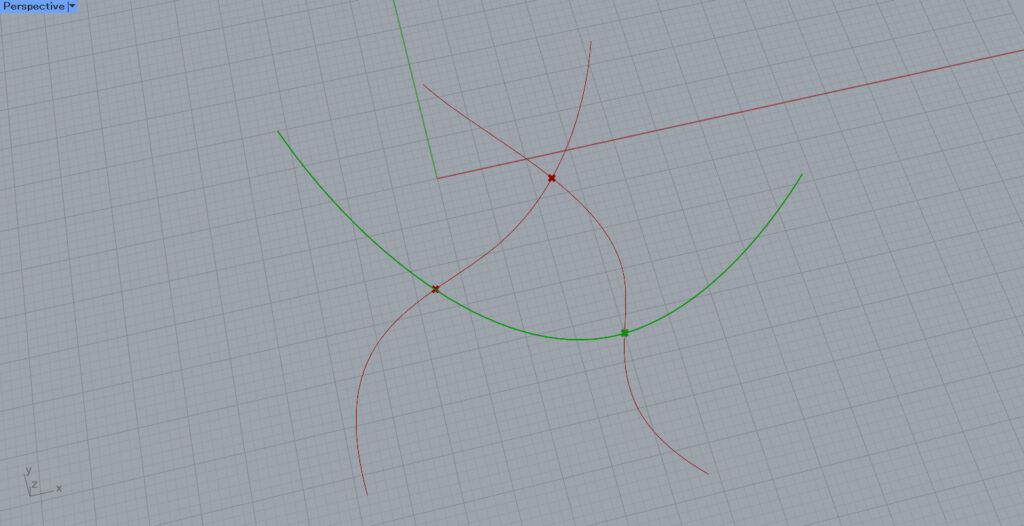
The second point of the first curve is selected.

Thus, from iA and iB, we can determine from the Index number which intersection point data is selected.

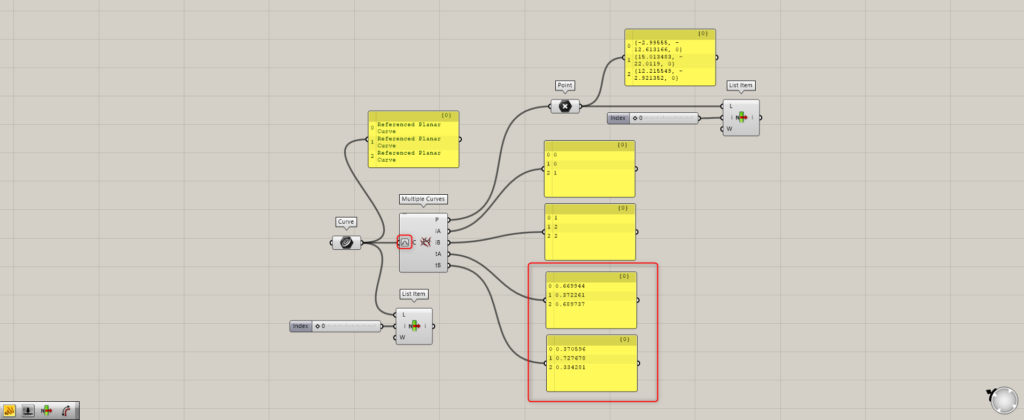
From tA and tB, we can determine the position of each curve, where the intersection is located.

Index number 0 is the first curve, index number 1 is the second curve, and index number 2 is the third curve.

In this case, the lengths of the curves are expressed as 0~1, since they are set to Reparameterize.