https://www.archdaily.com/543440/formstelle-format-elf-architekten
今回は、グラスホッパーで六角形の大きさが徐々に変わる、Formstelleの外観を再現しました。
動画で見る
全体の様子


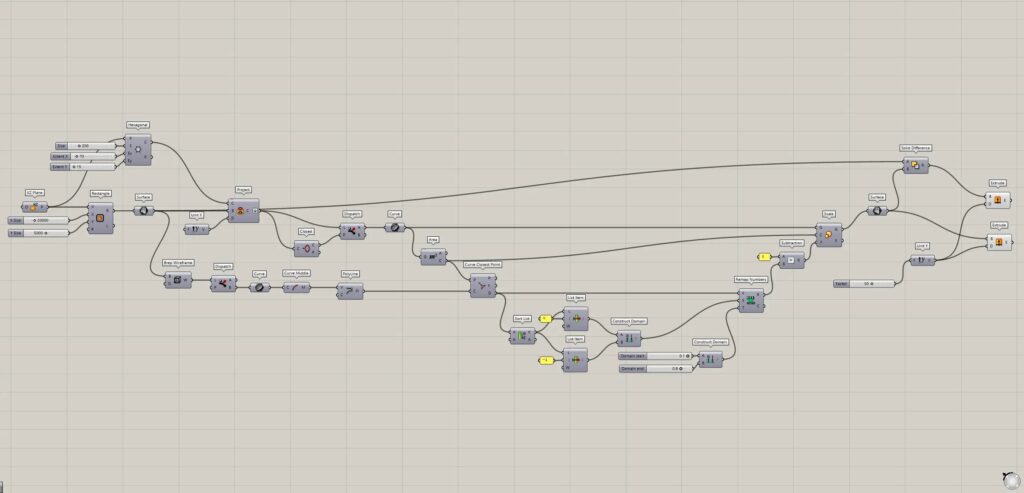
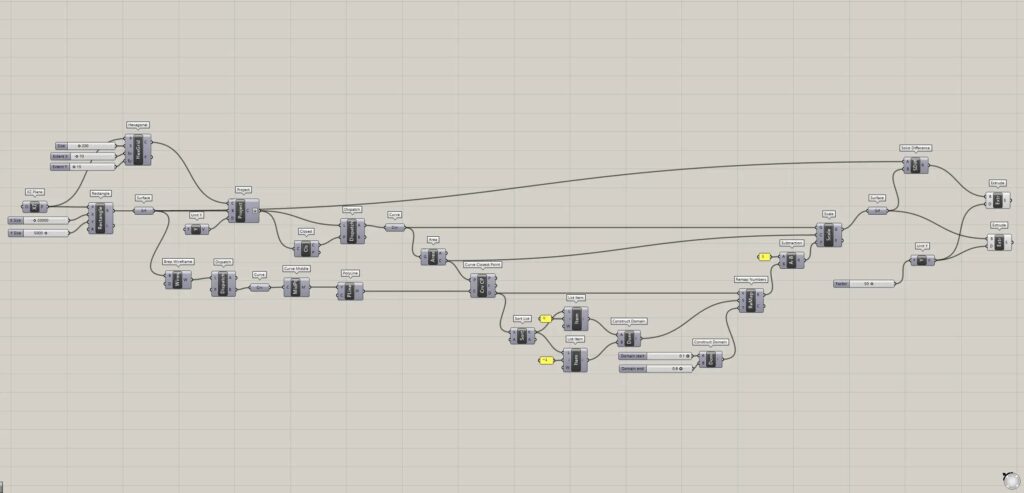
上2枚の画像は、グラスホッパーの様子です。


上2枚の画像は、ライノセラス上に書き出した様子です。

上の画像は、最終的にレンダリングした様子です。
それでは、順番に解説していきます。
今回使用したグラスホッパーとライノセラスのデータダウンロードはこちら
ダウンロードできるデータのご利用に関しては、利用規約をご覧ください。
全体コンポーネント
全体コンポーネント:①XZ Plane ②Rectangle ③Surface ④Hexagonal ⑤Unit Y ⑥Project ⑦Closed ⑧Dispatch ⑨Curve ⑩Area ⑪Brep Wireframe ⑫Curve Middle ⑬PolyLine ⑭Curve Closest Point ⑮Sort List ⑯List Item ⑰Construct Domain ⑱Remap Numbers ⑲Subtraction ⑳Scale ㉑Solid Difference ㉒Extrude
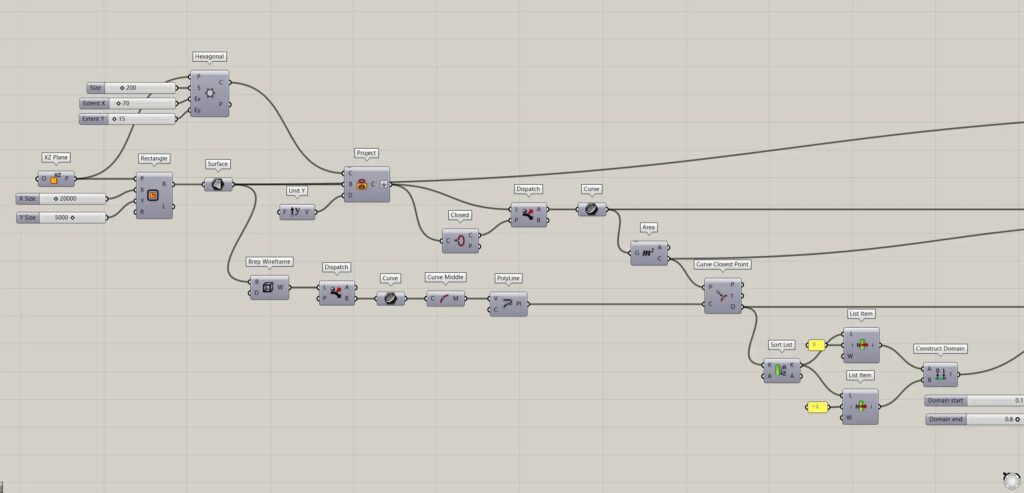
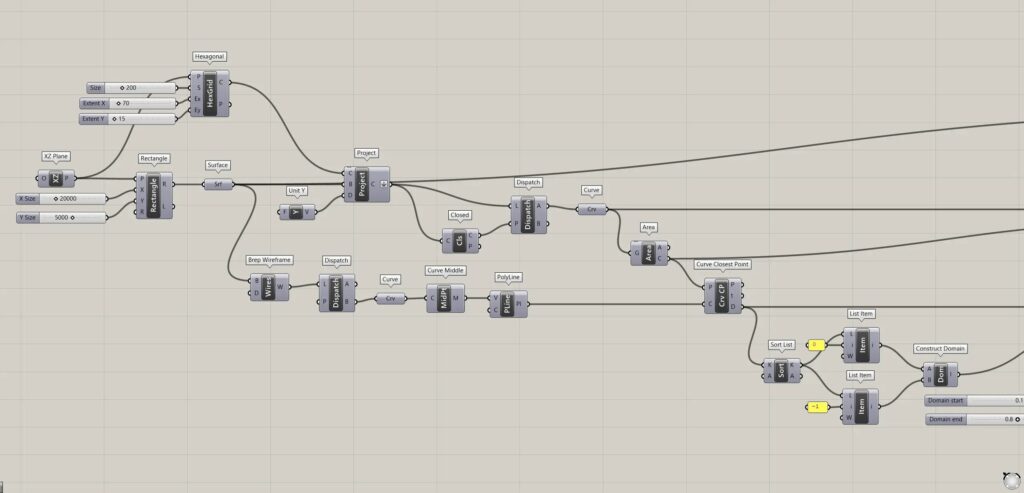
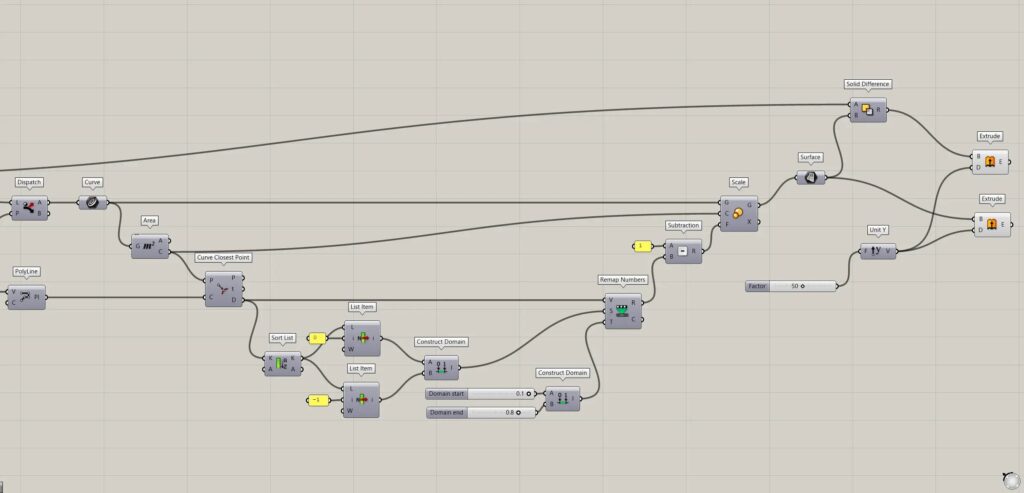
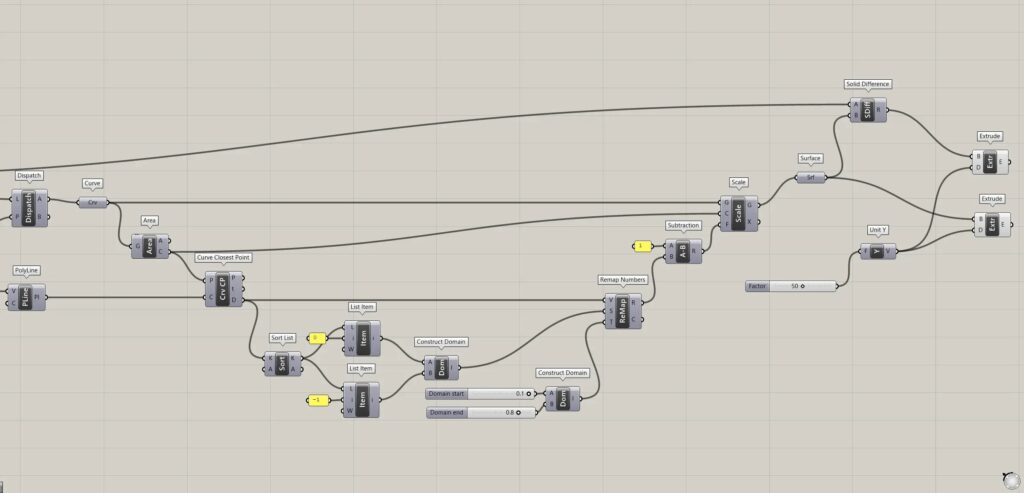
六角形の線データを作成する
最初に、六角形の線データを作成していきます。

最初に、XZ Planeを用意します。
これにより、X方向とY方向からできる作業平面が作成されます。
その後、XZ Planeを、RectangleのP端子につなげます。
その後、RectangleのXとY端子に、辺の長さの数値を入力します。
今回は、X端子に20000、Y端子に5000の数値を入力しています。
すると、上の画像のように、XZ作業平面上に長方形の線データが作成されました。

その後、RectangleのR端子を、Surfaceにつなげます。
すると、上の画像のように、長方形の線データから、長方形のサーフェスが作成されました。

その後、XZ Planeを、HexagonalのP端子につなげます。
そして、HexagonalのS端子に、六角形の半径の数値を入力します。
今回は、200の数値を入力しています。
さらに、HexagonalのExとEy端子に、それぞれの方向の六角形の個数の数値を入力します。
今回は、Ex端子に70、Ey端子に15の数値を入力しています。
すると、上の画像のように、半径200の六角形が、70×15の分だけ作成されました。

その後、HexagonalのC端子を、ProjectのC端子につなげます。
さらに、Surfaceを、ProjectのB端子につなげます。
そして、サーフェスに投影する方向のベクトルデータを、ProjectのD端子につなげます。
今回は、Unit Yをつなげ、Y方向のベクトルデータをつなげています。
すると、上の画像のように、サーフェスに六角形の線データが投影されました。
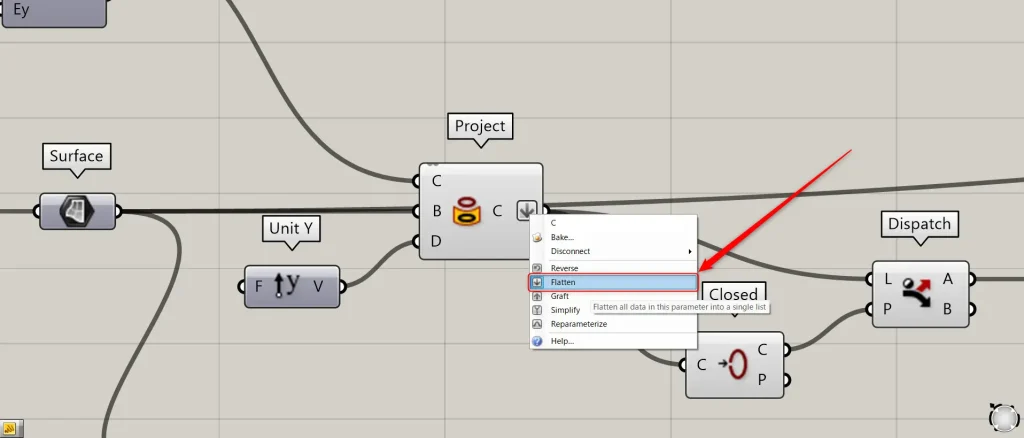
この際に、ProjectのC端子を右クリックし、Flattenに設定してください。
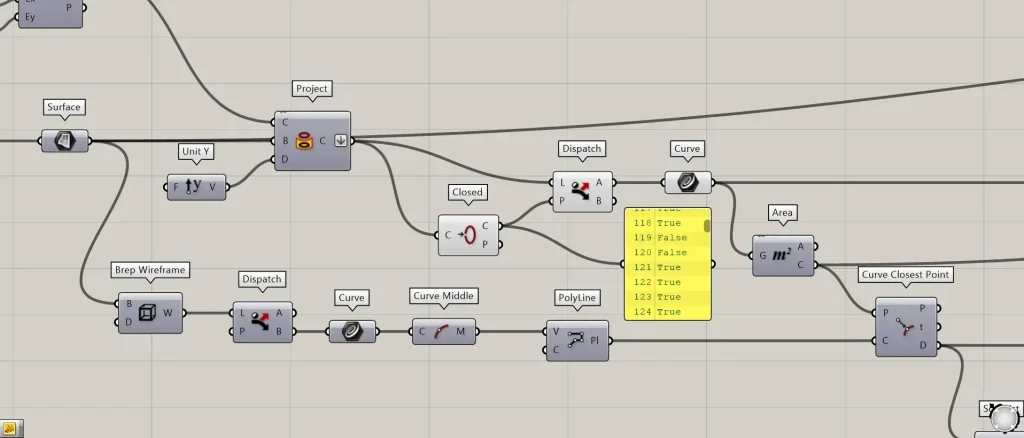
その後、Projectを、ClosedのC端子につなげます。
すると、ClosedのC端子から、六角形が閉じている場合True、開いている場合はFalseのデータが出力されます。
今回の場合、外側のいくつかの六角形は、一部分欠けているため、Falseと出力されます。
その後、ClosedのC端子を、DispatchのP端子につなげます。
さらに、Projectを、DispatchのL端子につなげます。
そして、DispatchのA端子を、Curveにつなげます。

すると、上の画像のように、閉じている六角形のみ取得することができました。
これで、六角形の線データを作成することができました。
上下に移動する程小さくなるようにスケールを変える
次に、上下に移動する程小さくなるようにスケールを変えていきます。

すると、上の画像のように、六角形の中心点を取得できます。

その後、Surfaceを、Brep WireframeのB端子につなげます。
すると、上の画像のように、長方形のサーフェスの枠線のデータを取得できました。

その後、Brep Wireframeを、DispatchのL端子につなげます。
その後、DispatchのB端子を、Curveにつなげます。
すると、奇数番目の枠線のみを取得できます。
そのため、上の画像のように、2つの縦方向の直線を取得できました。

その後、Curveを、Curve Middleにつなげます。
すると、2つの直線の中点を取得できます。

その後、Curve Middleを、PolyLineのV端子につなげます。
すると、上の画像のように、取得した中点をつなぐ直線を作成できました。
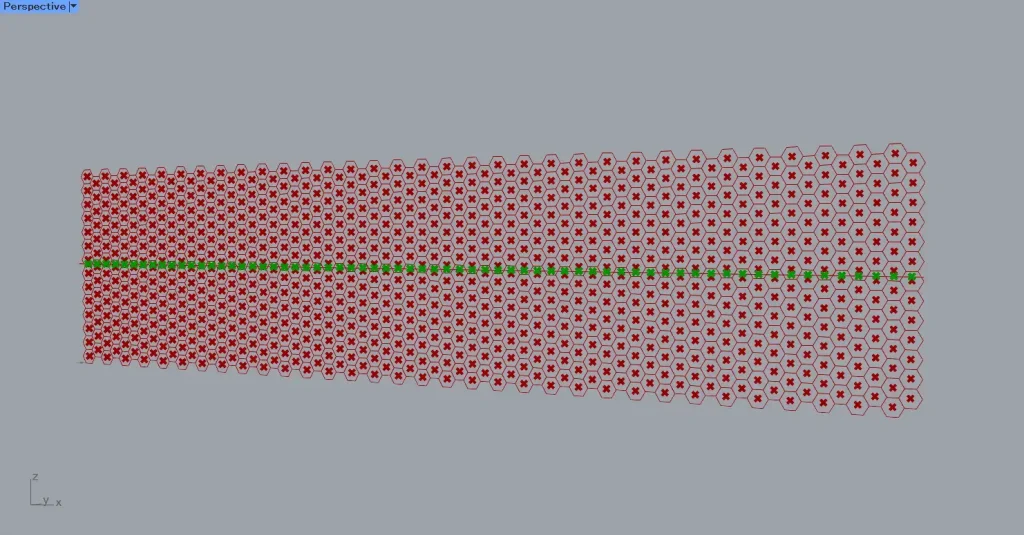
その後、PolyLineを、Curve Closest PointのC端子につなげます。
さらに、AreaのC端子を、Curve Closest PointのP端子につなげます。
すると、六角形の中心点が、直線に最も近い位置に移動しました。
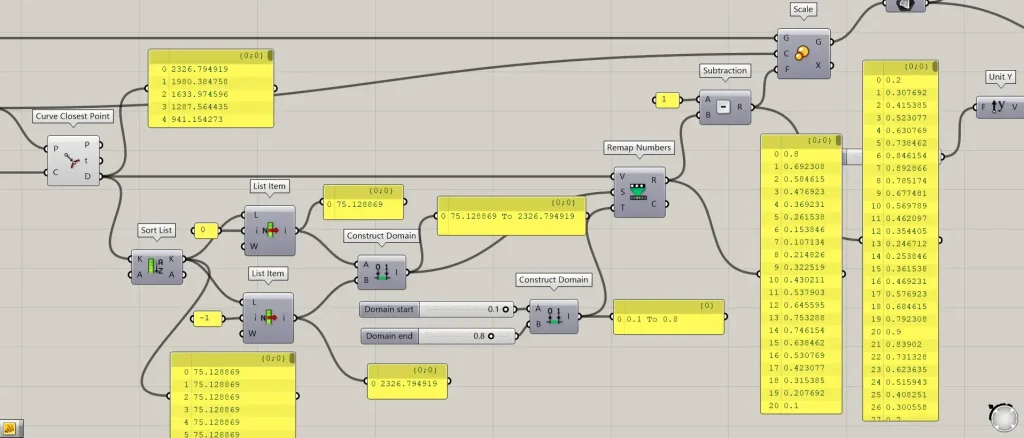
次に、スケールを変える数値を作成していきます。
Curve Closest PointのD端子からは、元々の六角形の中心点から、移動した点までの距離の数値が出力されます。
Curve Closest PointのD端子を、Sort ListのK端子につなげます。
すると、取得した距離の数値が、小さい順に並び替えられました。
その後、Sort ListのK端子を、2つのList ItemのL端子につなげます。
そして、1つ目のList Itemのi端子には、0の数値を入力します。
2つ目のList Itemのi端子には、-1の数値を入力します。
0を入力した方からは、一番小さい距離の数値が出力されます。
-1を入力した方からは、一番大きい距離の数値が出力されます。
その後、0を入力した方のList Itemを、Construct PointのA端子につなげます。
その後、-1を入力した方のList Itemを、Construct PointのB端子につなげます。
すると、距離の最小値と最大値の数値範囲が作成されます。
その後、スケールの倍率の最小値の数値を、新たなConstruct DomainのA端子につなげます。
今回は、0.1の数値を入力しています。
さらに、スケールの倍率の最大値の数値を、新たなConstruct DomainのB端子につなげます。
今回は、0.8の数値を入力しています。
すると、0.1 To 0.8という数値範囲が作成されました。
その後、スケールの数値を入力したConstruct Domainを、Remap NumbersのT端子につなげます。
さらに、距離の数値範囲の方のConstruct Domainを、Remap NumbersのS端子につなげます。
さらに、Curve Closest PointのD端子を、Remap NumbersのV端子につなげます。
すると、距離の数値が、0.1~0.8の数値範囲に対応して数値が変わりました。
しかし、この数値のままでスケールを変えると、上下に移動する程大きくなるスケールの倍率の数値になってしまいます。
1の数値を、SubtractionのA端子につなげます。
さらに、Remap NumbersのR端子を、SubtractionのB端子につなげます。
すると、1の数値から作成した数値で引き算することができました。
これで、上下に移動する程小さくなるスケールの倍率の数値に変えることができました。

その後、Subtractionを、ScaleのF端子につなげます。
さらに、AreaのC端子を、ScaleのC端子につなげます。
すると、上の画像のように、六角形が上下に移動する程小さくなりました。

すると、上の画像のように、スケールを変えた六角形の線データから、サーフェスを作成することができました。
これで、上下に移動する程小さくなるようにスケールを変えることができました。
サーフェスに穴を開けて厚みを付ける
最後に、サーフェスに穴を開けて厚みを付けていきます。

Surfaceを、Solid DifferenceのB端子につなげます。
さらに、一番最初に使用したSurfaceを、Solid DifferenceのA端子につなげます。
すると、上の画像のように、スケールを変えた六角形で、サーフェスに穴を開けることができました。

その後、厚みの数値を、Unit Yにつなげます。
今回は、50の数値を入力しています。
その後、2つのExtrudeのD端子に、Unit Yをつなげます。
そして、SurfaceとSolid Differenceを、それぞれExtrudeのB端子につなげます。
すると、上の画像のように、穴を開けたサーフェスと六角形のサーフェスに厚みを付けることができました。
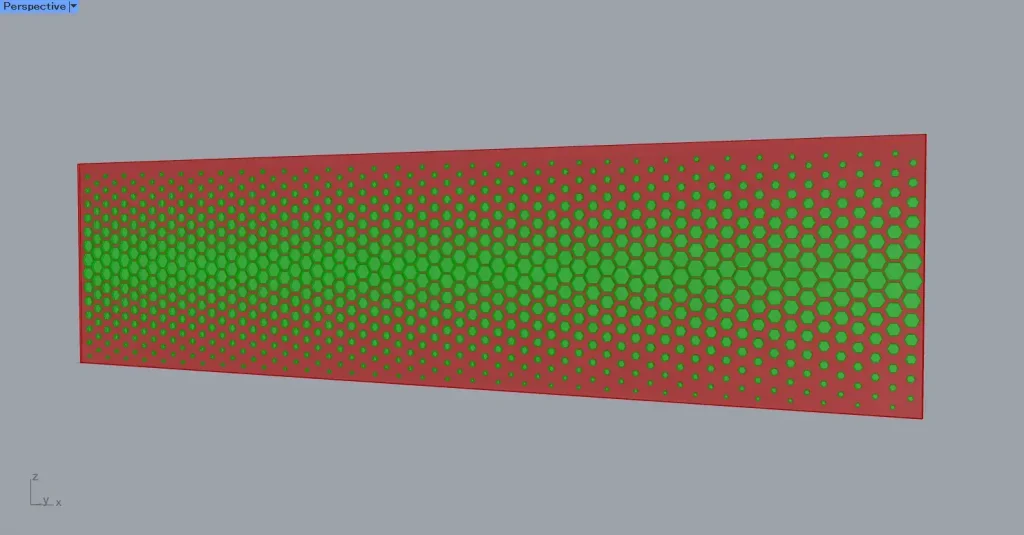
これで完成です。
今回は以上になります。







Comment