https://en.wikipedia.org/wiki/Selfridges_Building,_Birmingham
今回は、グラスホッパーでイギリスにあるセルフリッジ ビルの外観を再現しました。
動画で見る
全体の様子

ライノセラスとグラスホッパーの様子です。

ズームした様子です。

ライノセラス上で、マテリアルを付けた様子です。

最終的にレンダリングした様子です。
それでは、順番に解説していきます。
今回使用したグラスホッパーとライノセラスのデータダウンロードはこちら
ダウンロードできるデータのご利用に関しては、利用規約をご覧ください。
全体コンポーネント

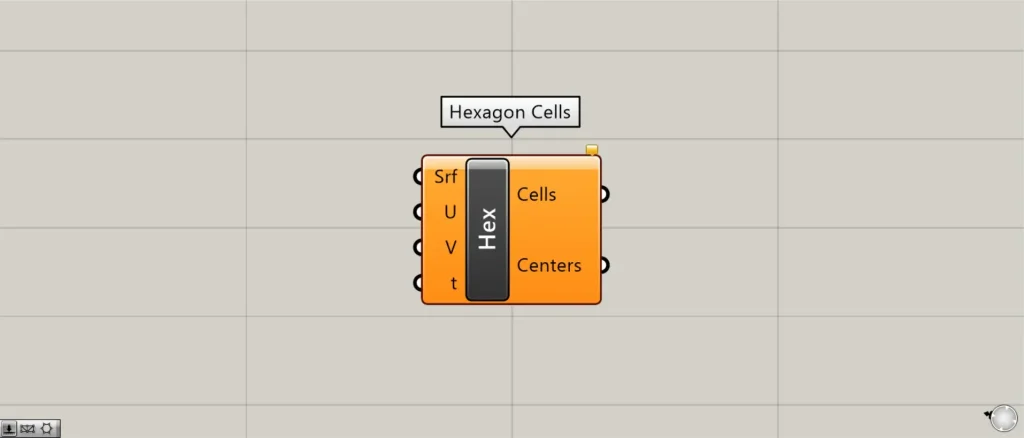
今回のプログラミングでは、プラグインであるLunch boxのHexagon Cellsコンポーネントを使用しています。
そのため、今回のプログラムを使用するには、Lunch boxのプラグインをインストールしてください。
詳しいダウンロード方法は下のサイトで解説されているので是非参考にしてください。
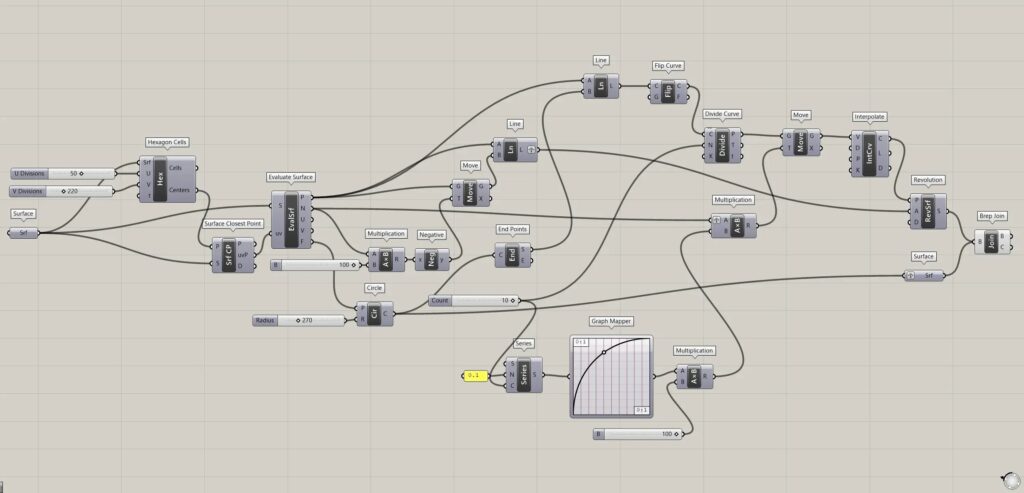
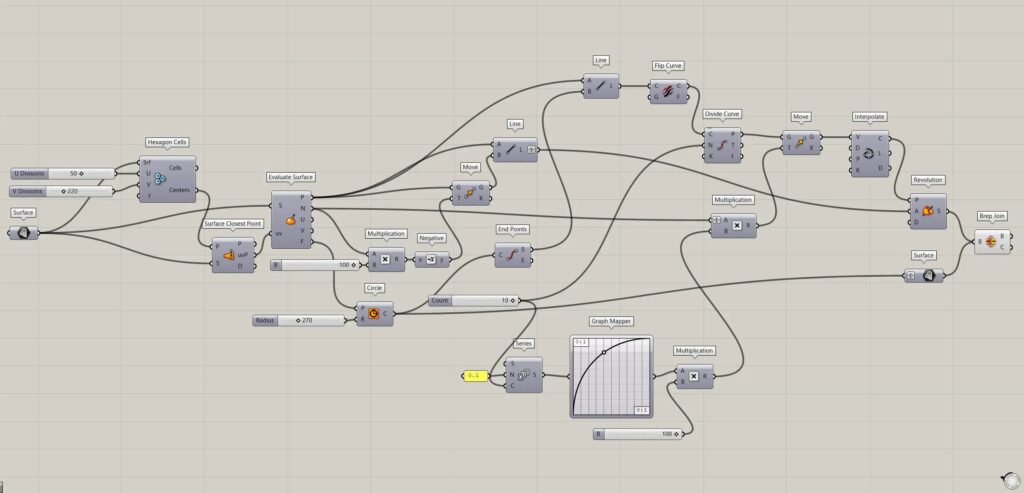
全体コンポーネント:①Surface ②Hexagon Cells ③Surface Closest Point ④Evaluate Surface ⑤Circle ⑥End Points ⑦Multiplication ⑧Negative ⑨Move ⑩Line ⑪Flip Curve ⑫Divide Curve ⑬Series ⑭Graph Mapper ⑮Interpolate ⑯Revolution ⑰Brep Join
サーフェス上に6角形を作成する
最初は、サーフェス上に6角形を作成していきます。
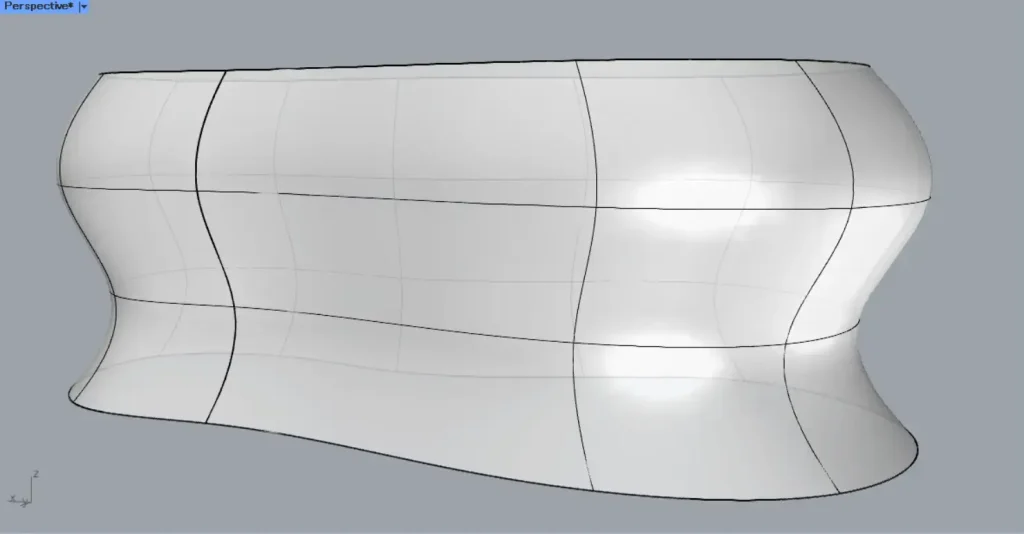
今回は、上の画像のライノセラス上のサーフェスを使用します。

最初は、Surfaceにライノセラス上のサーフェスを格納します。

その後、Surfaceを、Hexagon CellsのSrf端子につなげます。
さらに、Hexagon CellsのUとV端子に、それぞれ縦と横方向に配置する数値を入力します。
今回は、50と220をそれぞれ入力しています。
すると、サーフェス上に六角形の線データが作成されました。

その後、Hexagon CellsのCenters端子を、Surface Closest PointのP端子につなげます。
さらに、Surfaceを、Surface Closest PointのS端子につなげます。
すると、六角形の中心の点が、サーフェス上に反映されます。

その後、Surface Closest PointのuvP端子を、Evaluate Surfaceのuv端子につなげます。
さらに、Surfaceを、Evaluate SurfaceのS端子につなげます。
すると、サーフェス上の点の位置の情報を取得することができます。
Evaluate SurfaceのP端子からは、点データが出力されます。
N端子からは、点の位置の法線のベクトルデータが出力されます。
F端子からは、点の位置の作業平面データが出力されます。


その後、Evaluate SurfaceのF端子を、CircleのP端子につなげます。
さらに、CircleのR端子に、半径の数値を入力します。
今回は、270を入力しています。
すると、上2枚の画像のように、円の線データが作成されました。
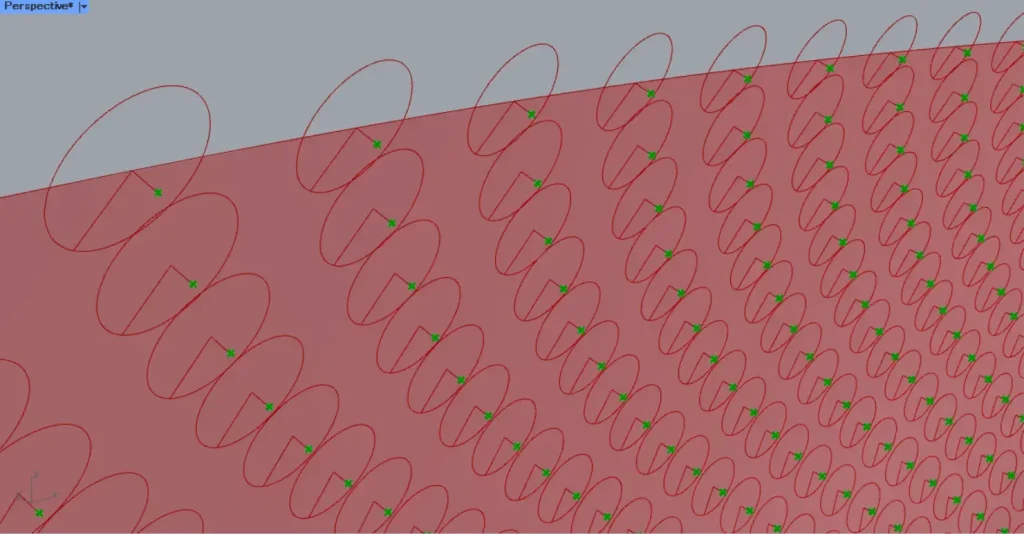
その後、Evaluate SurfaceのN端子を、MultiplicationのA端子につなげます。
さらに、円の中心点を移動させる距離の数値を、MultiplicationのB端子につなげます。
今回は、100を入力しています。
さらに、MultiplicationをNegativeにつなげ、数値をマイナスにします。
また、Evaluate SurfaceのP端子を、MoveのG端子につなげます。
すると、上の画像のように、点が移動しました。
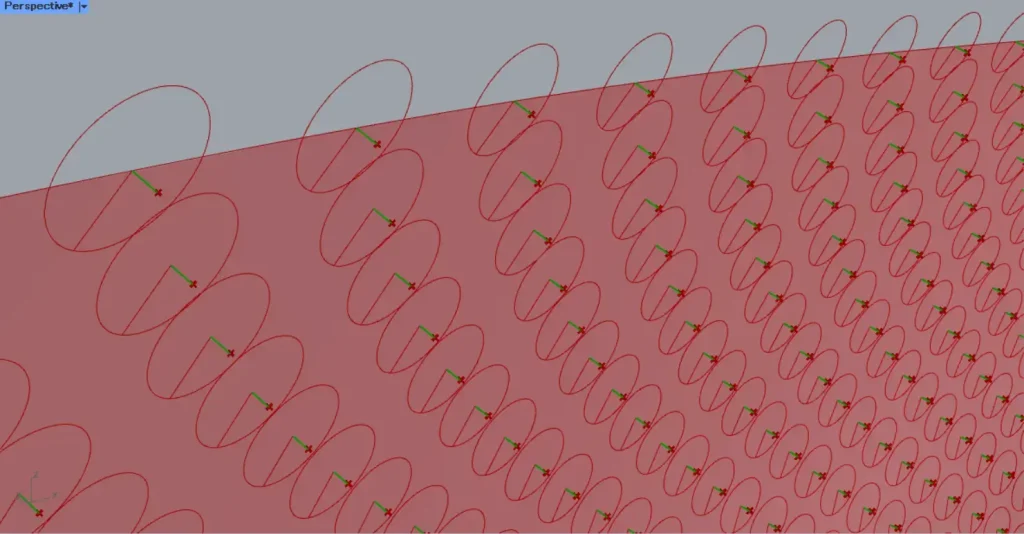
その後、Evaluate SurfaceのP端子とMoveのG端子を、Lineにつなげます。
すると、上の画像のような直線が作成されました。
これらの直線は、後で回転軸として使います。
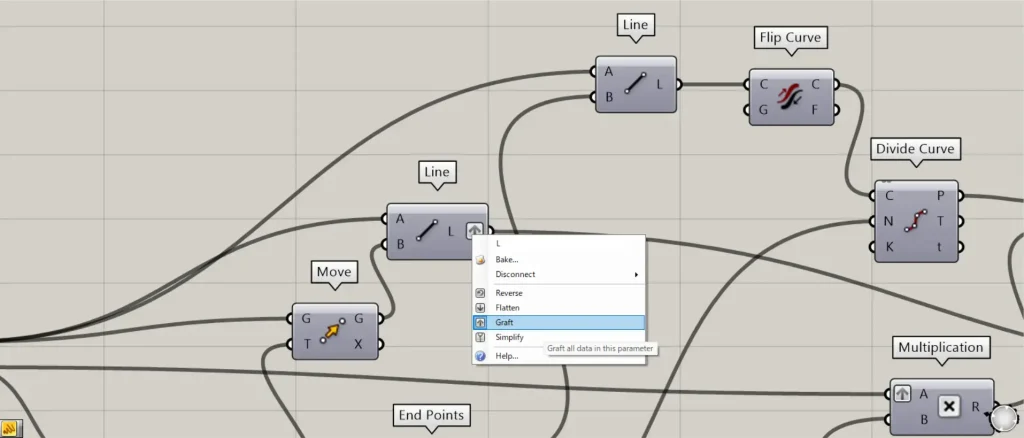
この際に、LineのL端子を右クリックし、Graftに設定してください。
その後、Circleを、End Pointsにつなげます。
すると、円上の点を取得できます。
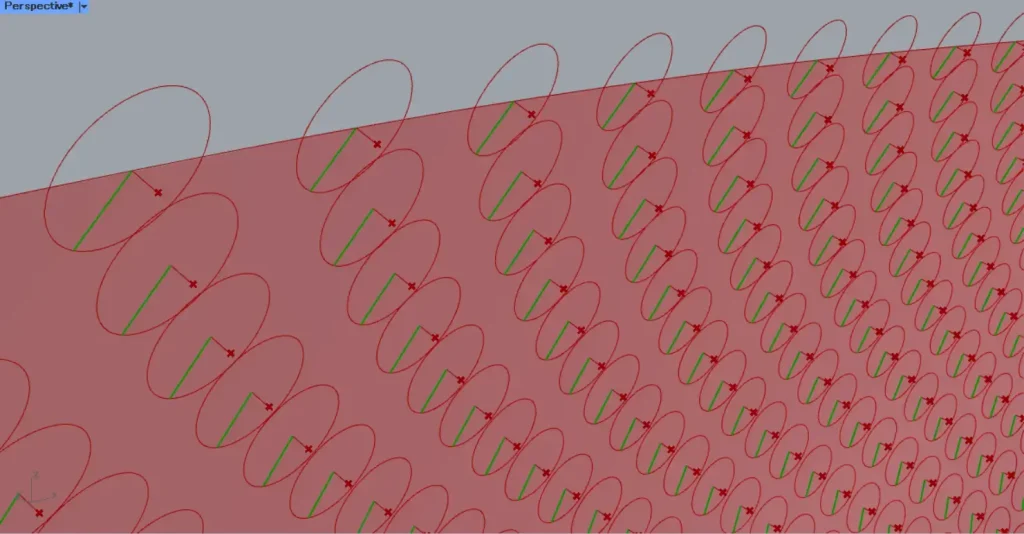
そして、Evaluate SurfaceのP端子とEnd PointsのS端子を、新たなLineにつなげます。
すると、上の画像のように、半径の直線が作成されました。
その後、Lineを、Flip CurveのC端子につなげます。
これは、後で移動させる向きを反対にするためです。
そして、Flip CurveのC端子を、Divide CurveのC端子につなげます。
そして、Divide CurveのN端子に、線の分割数の数値を入力します。
今回は、10を入力しています。
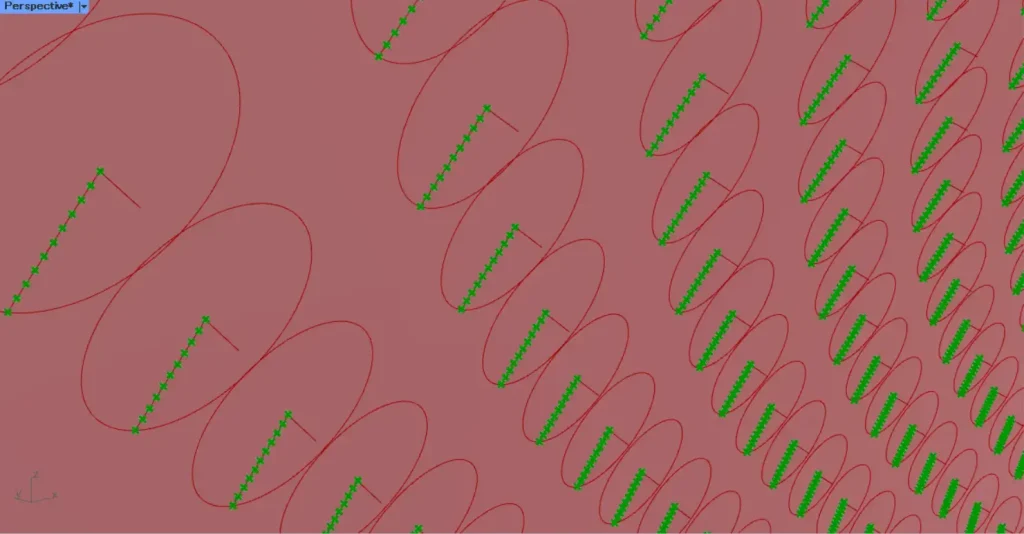
すると、直線を10個に分割する位置に、点が作成されました。
その後、Divide CurveのN端子に入力した10を、SeriesのC端子につなげます。
そして、SeriesのN端子に、0.1を入力します。
すると、0~0.9までの数値が10個作成されます。
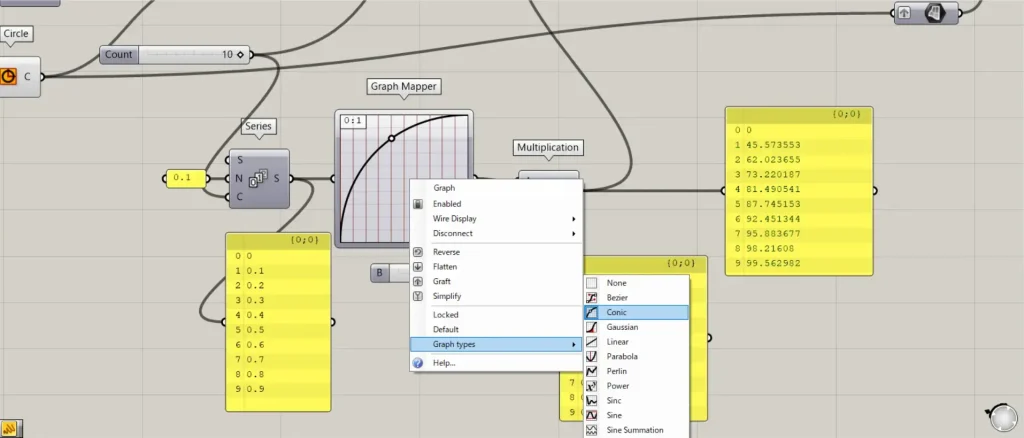
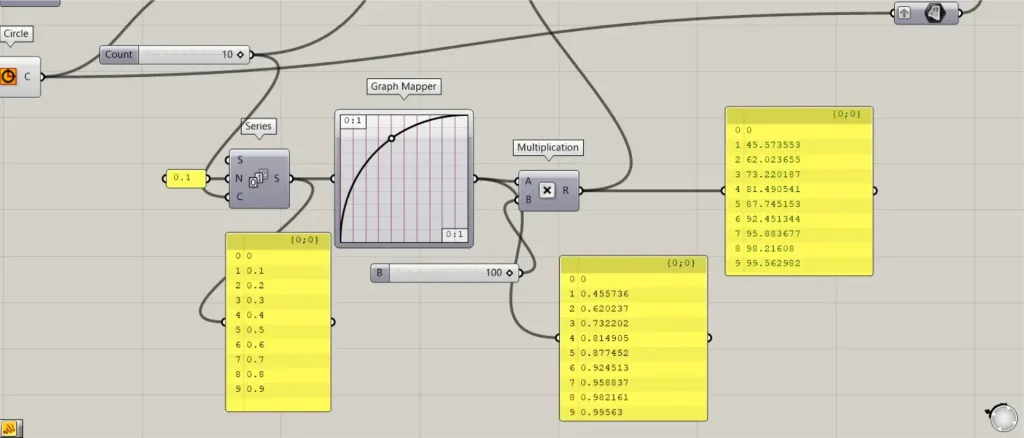
その後、Seriesを、Graph Mapperにつなげます。
そして、Graph Mapperを右クリックし、Graph typesからConicを選択します。
そして、グラフの形を、上の画像のようにします。
その後、Graph Mapperを、MultiplicationのA端子につなげます。
さらに、任意の倍率の数値を、B端子につなげます。
今回は、100を入力しています。
そして、Multiplicationを、新たなMultiplicationのB端子につなげます。
さらに、Evaluate SurfaceのN端子を、MultiplicationのA端子につなげます。
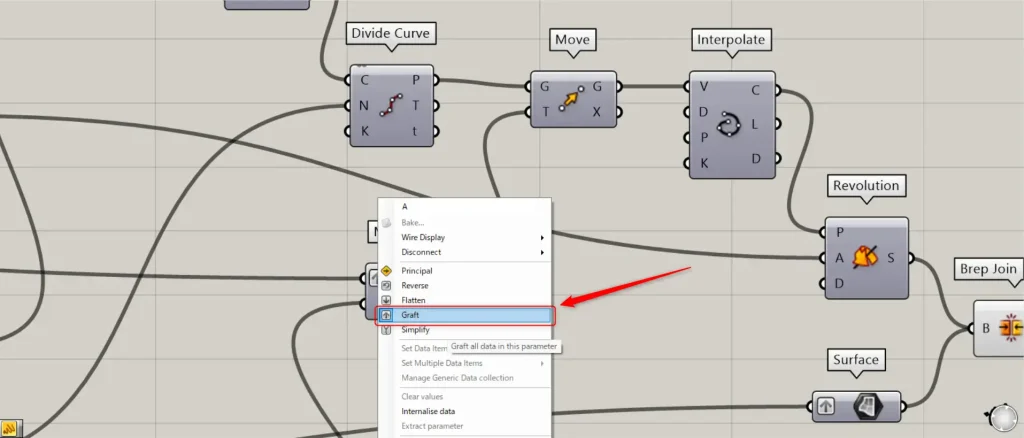
この際に、MultiplicationのA端子を右クリックし、Graftを選択してください。
その後、Multiplicationを、MoveのT端子につなげます。
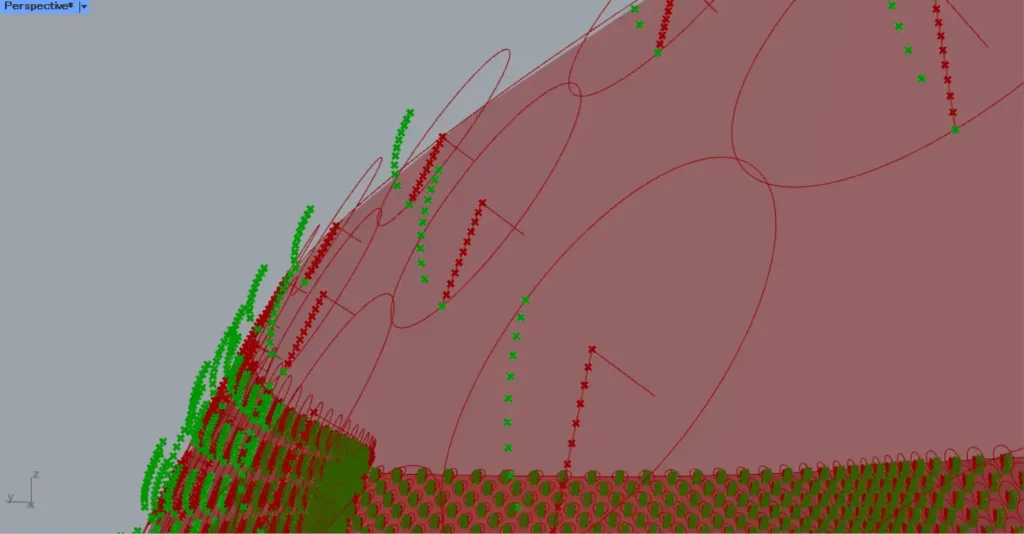
また、Divide CurveのP端子を、MoveのG端子につなげます。
すると、上の画像のように、点が段々と移動します。
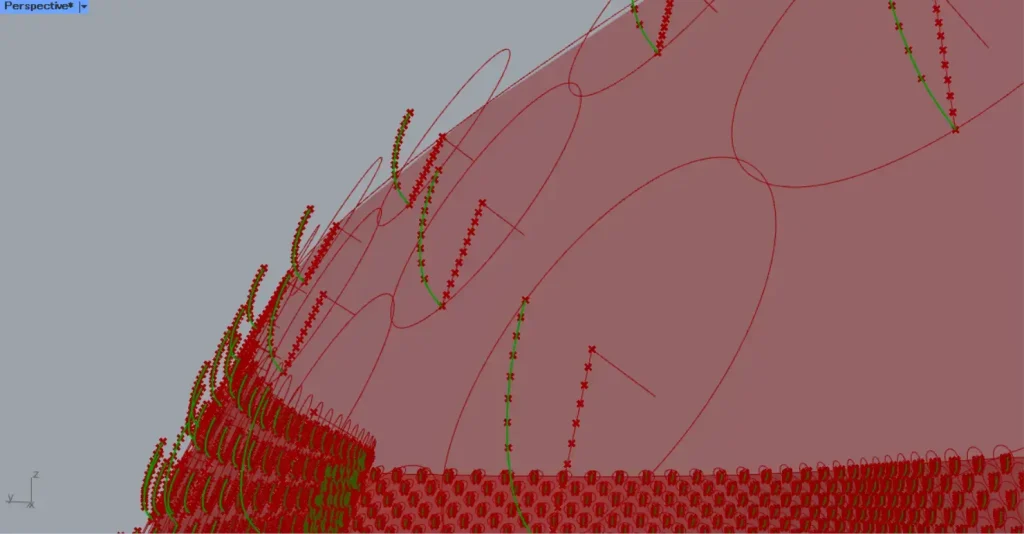
そして、MoveのG端子を、InterpolateのV端子につなげます。
すると、点をつなぐ曲線が作成されます。
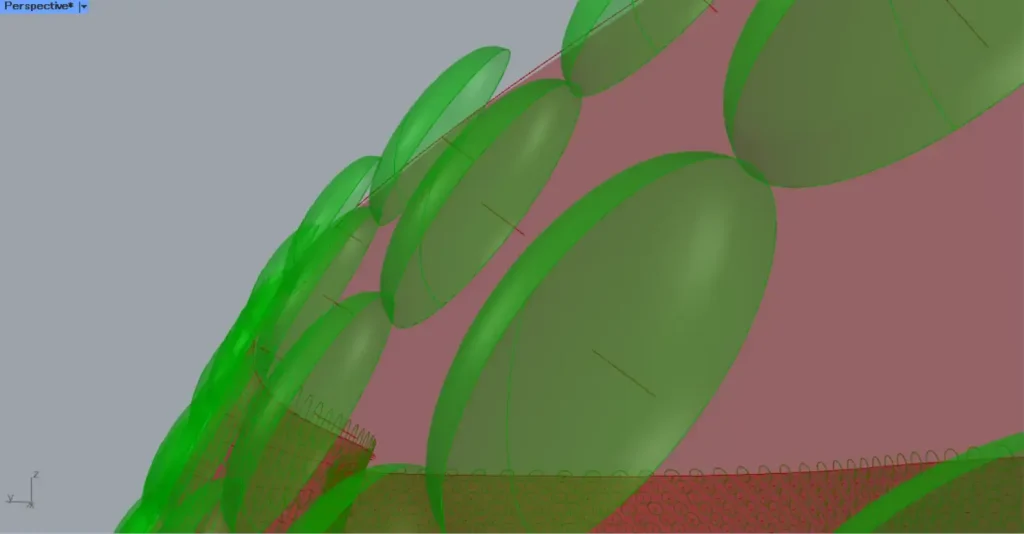
その後、InterpolateのC端子を、RevolutionのP端子につなげます。
そして、GraftしているLineをRevolutionのA端子につなげます。
すると、Lineの直線を回転軸として、回転体が作成されます。
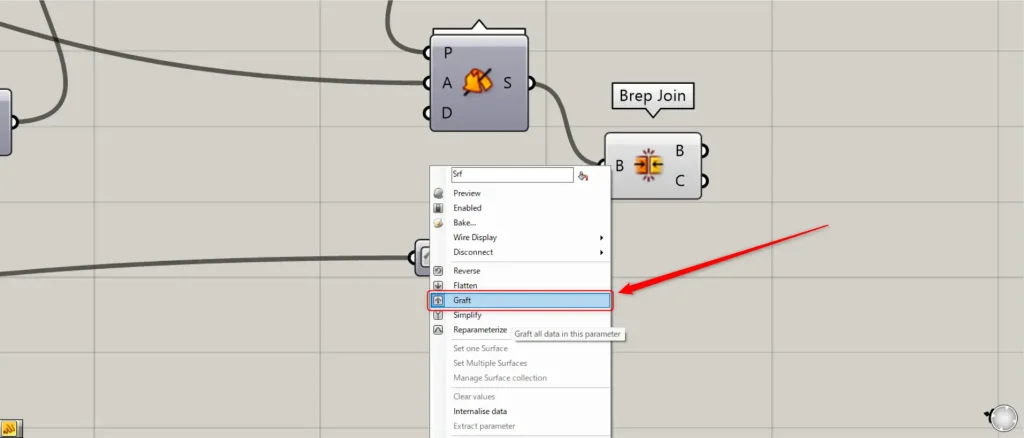
その後、Circleを、Surfaceにつなげてサーフェスに変換します。
この際に、Surfaceを右クリックし、Graftに設定してください。

そして、RevolutionとSurfaceを、Brep Joinにつなげます。
すると、円と回転体が結合します。

これで完成です。
今回は以上になります。







Comment