今回は、グラスホッパーで巻貝をイメージしたパビリオンの作成方法について解説します。
動画で見る
全体の様子

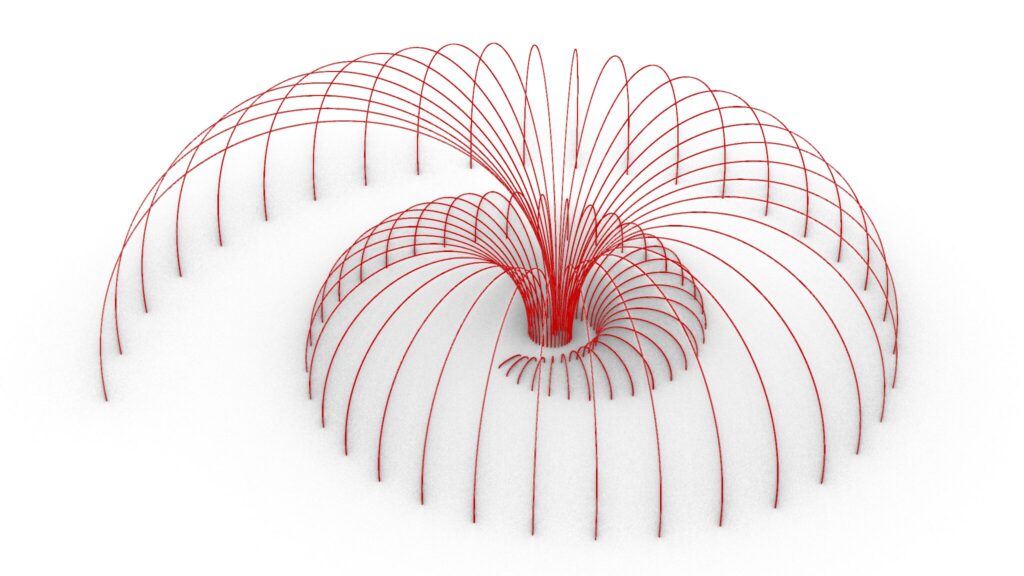


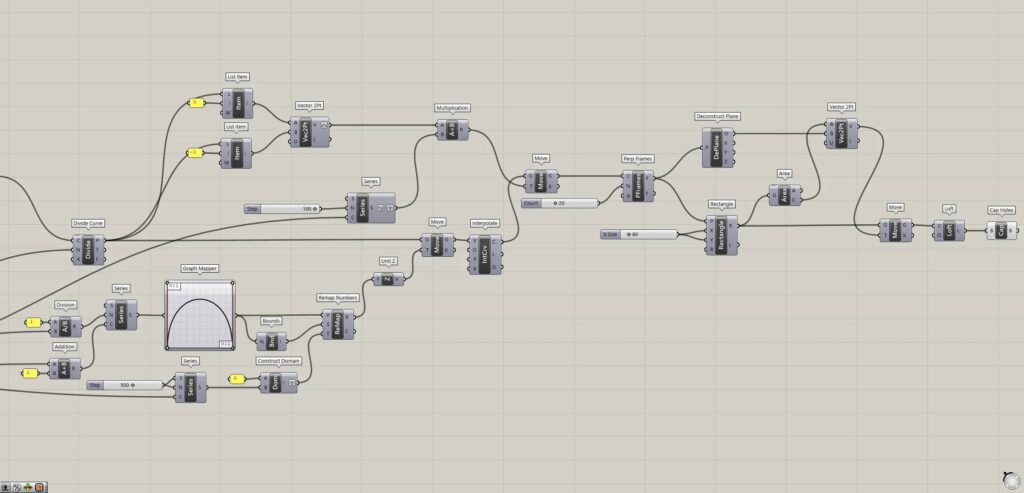
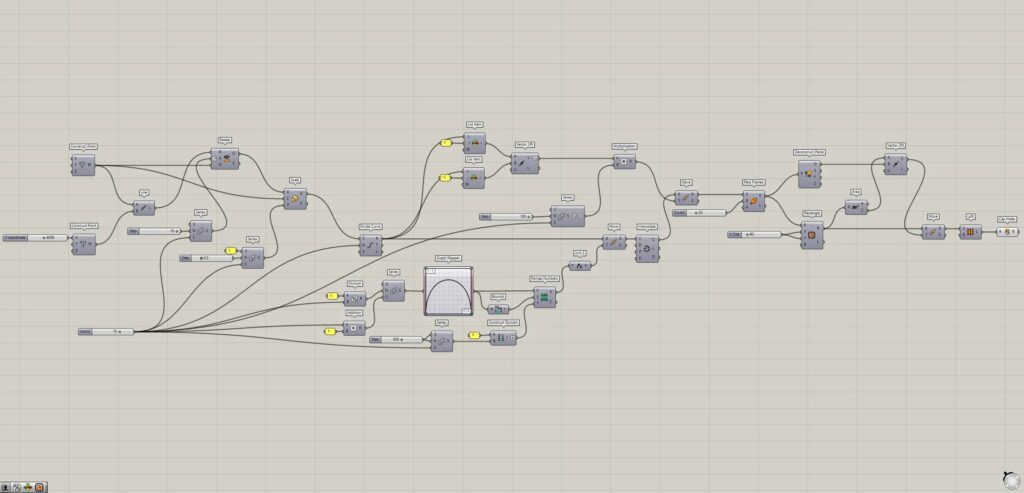
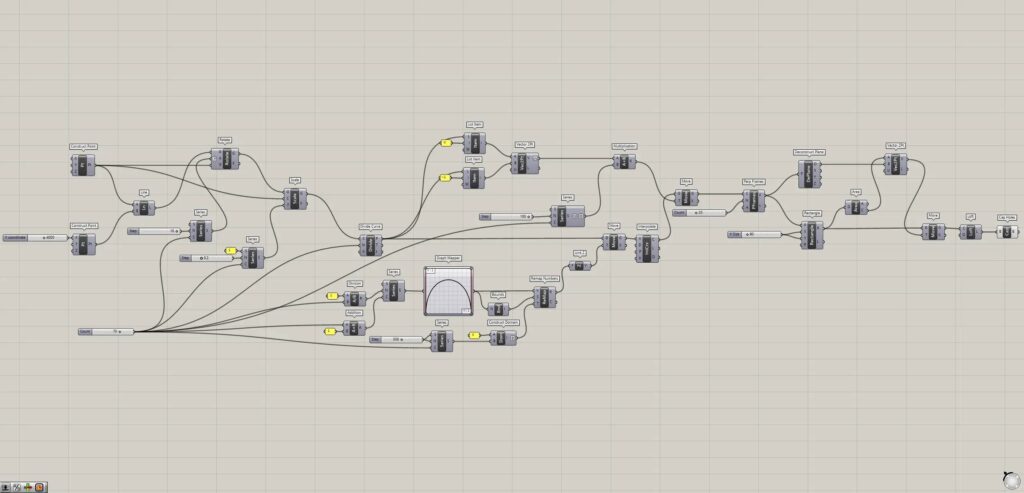
上4枚の画像は、グラスホッパーの様子です。




上4枚の画像は、ライノセラス上に書き出して色を付けた様子です。

上の画像は、最終的にレンダリングした様子です。
それでは、順番に解説していきます。
今回使用したグラスホッパーとライノセラスのデータダウンロードはこちら
ダウンロードできるデータのご利用に関しては、利用規約をご覧ください。
全体コンポーネント
全体コンポーネント:①Construct Point ②Line ③Rotate ④Series ⑤Scale ⑥Divide Curve ⑦Division ⑧Addition ⑨Graph Mapper ⑩Bounds ⑪Construct Domain ⑫Remap Numbers ⑬Unit Z ⑭Move ⑮Interpolate ⑯List Item ⑰Vector 2Pt ⑱Multiplication ⑲Perp Frames ⑳Rectangle ㉑Area ㉒Deconstruct Plane ㉓Loft ㉔Cap Holes
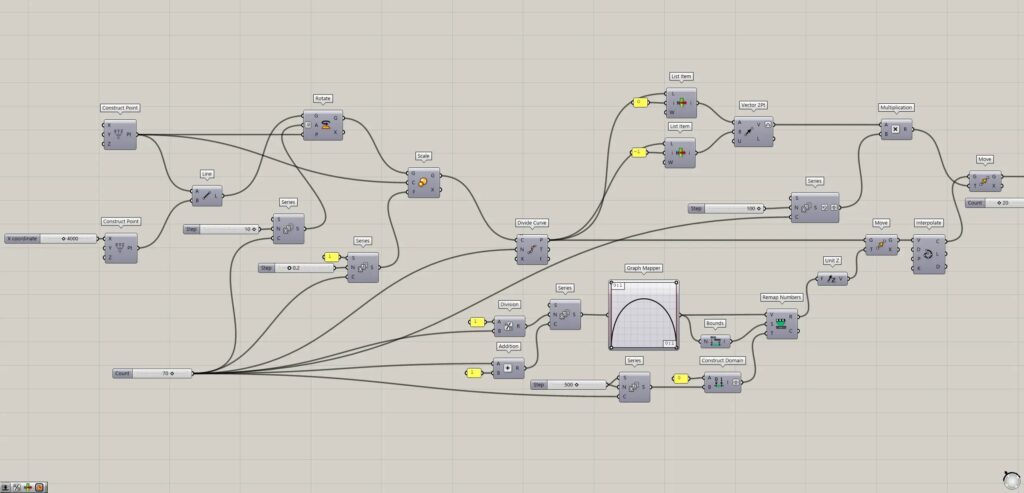
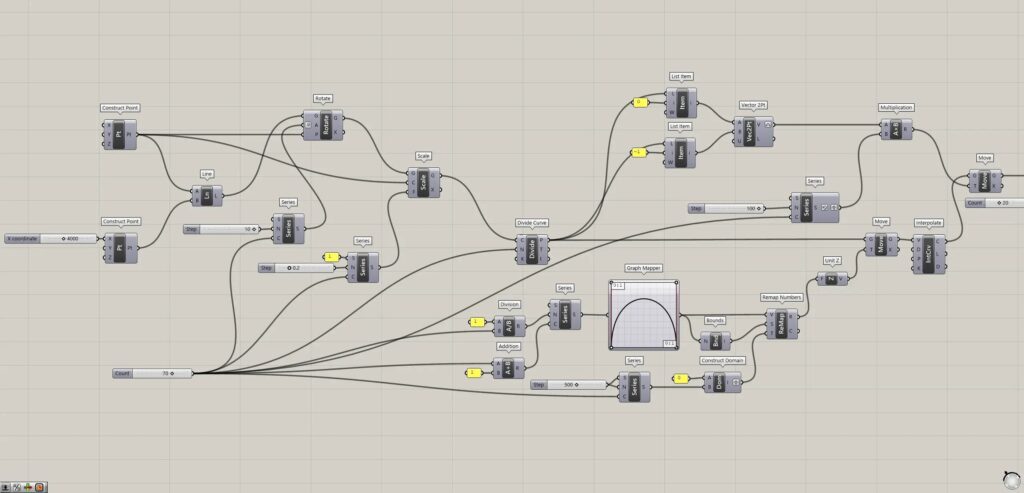
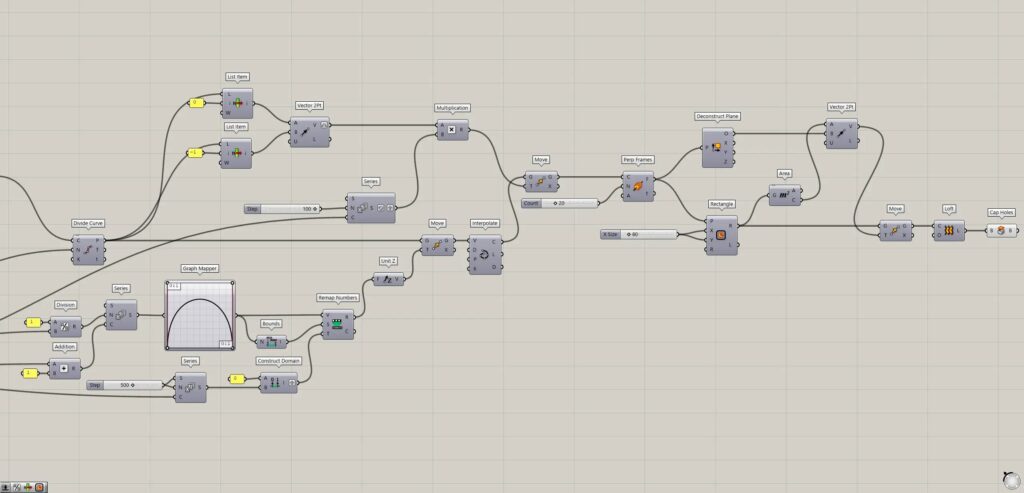
線を回転してスケールを変える
最初に、線を回転させ、さらにスケールを変えていきます。

2つのConstruct Pointを配置します。
1つはそのままで、2つ目の方は、Construct(X)にX座標の数値を入力します。
今回は、4000を入力しています。
すると、上の画像のように、0,0,0と4000,0,0の座標に点が作成されました。

その後、2つのConstruct Pointを、Lineにつなげます。
すると、上の画像のように、2つの点をつなぐ線が作成されます。
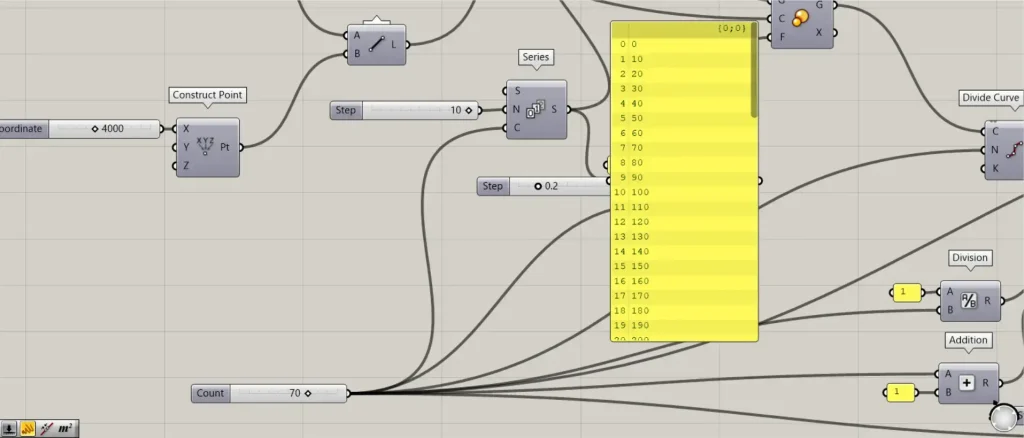
次に、回転させる角度の数値を作成していきます。
個数の数値を、Series(C)につなげます。
今回は、70を入力しています。
さらに、角度の数値を、Series(N)につなげます。
今回は、10を入力しています。
すると、0から10ずつ増加する数値が、70個作成されます。
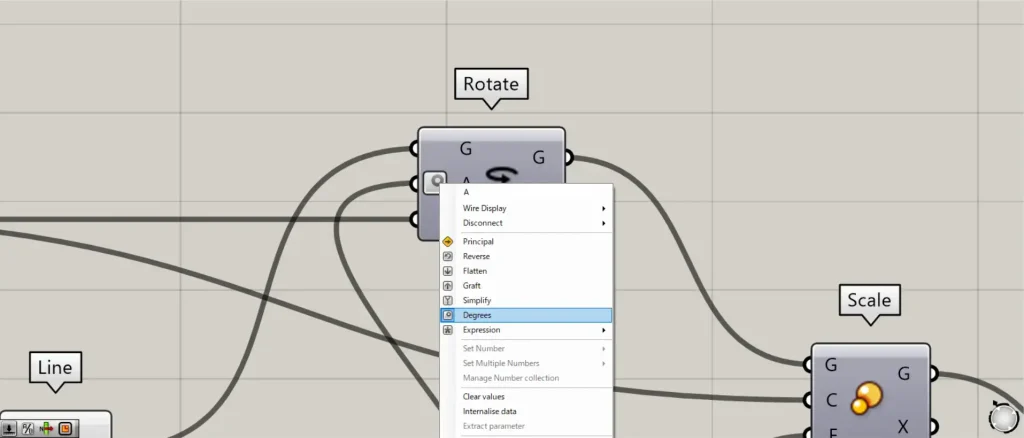
この際に、Rotate(A)を右クリックし、Degreesに設定してください。
さらに、先程の何も入力していない方のConstruct Pointを、Rotate(P)につなげます。

すると、上の画像のように、線が回転コピーされます。
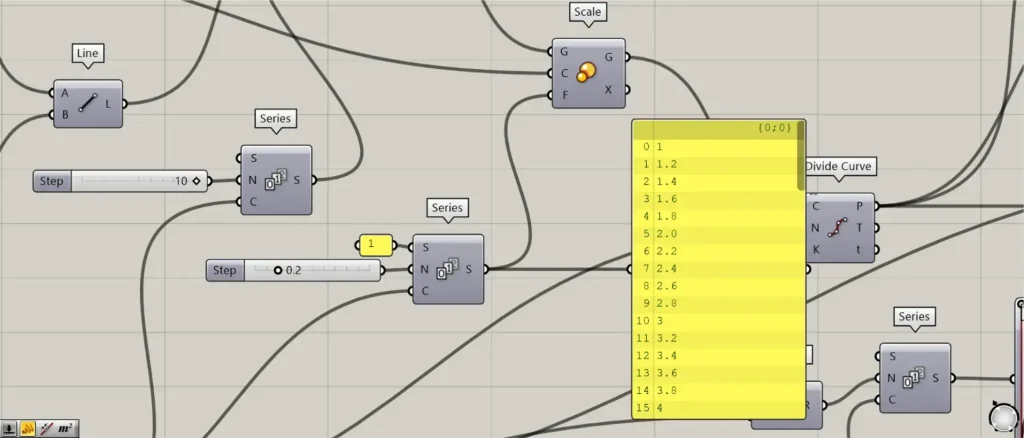
次に、スケールを変える数値を作成します。
先程の70のを、Series(C)につなげます。
さらに、1を、Series(S)につなげます。
さらに、0.2を、Series(N)につなげます。
すると、1から0.2ずつ増加する数値が、70個作成されます。

さらに、先程の何も入力していない方のConstruct Pointを、Scale(C)につなげます。
さらに、Rotate(G)を、Scale(G)につなげます。
すると、上の画像のように、線のスケールが1本ずつ変わりました。
アーチ状の線を作成する
次に、アーチ状の線を作成していきます。

Scale(G)を、Divide Curve(C)につなげます。
さらに、分割数の数値を、Divide Curve(N)につなげます。
今回は、先程の70を入力しています。
すると、上の画像のように、各線が70に分割される位置に、点が作成されます。
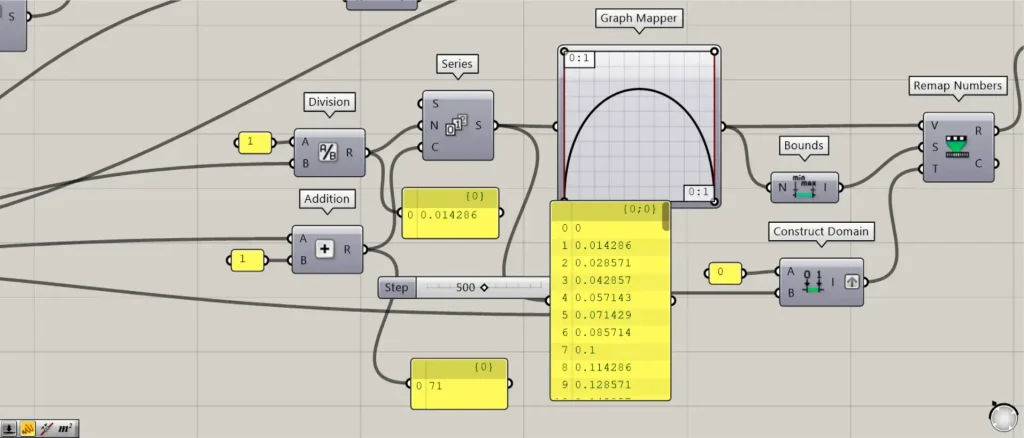
その後、先程の70を、Division(B)につなげます。
さらに、1をDivision(A)につなげます。
すると、1÷70の数値が出力されます。
この数値は、後で使うグラフのX軸の数値になります。
さらに、先程の70と1を、Additionにつなげます。
すると、70+1=71が出力されます。
これは、点の個数が71個なので、1を足しています。
その後、Divisionを、Series(N)につなげます。
さらに、Additionを、Series(C)につなげます。
すると、0から1/70ずつ増加する数値が、71個作成されます。
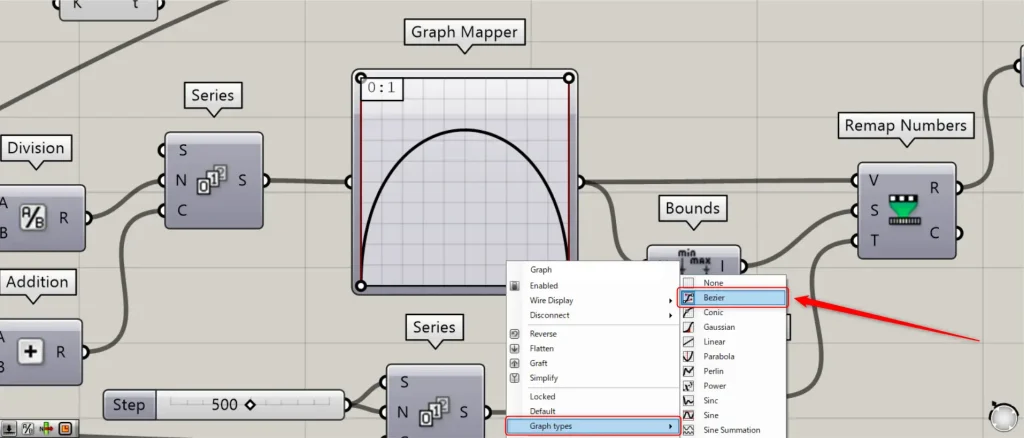
その後、Seriesを、Graph Mapperにつなげます。
この際に、Graph Mapperを右クリックし、Graph typesからBezierに設定してください。
さらに、上の画像を参考に、グラフの形を設定してください。
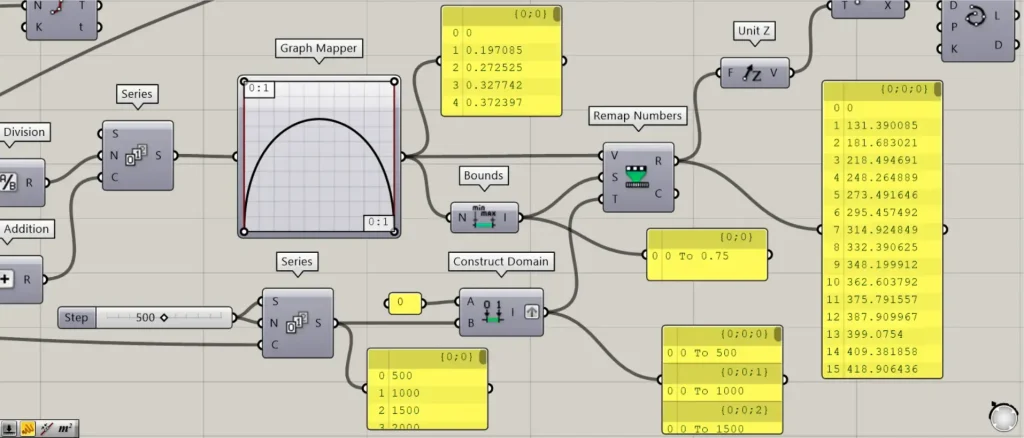
すると、Graph Mapperから、入力したX軸の数値に該当するY軸の数値が出力されます。
その後、Graph Mapperを、Boundsにつなげます。
すると、Graph Mapperから出力される数値の、最小値と最大値から構成される数値範囲が作成されます。
その後、先程の70を、Series(C)につなげます。
さらに、500を、Series(SとN)につなげます。
すると、500から500ずつ増加する数値が、70個作成されます。
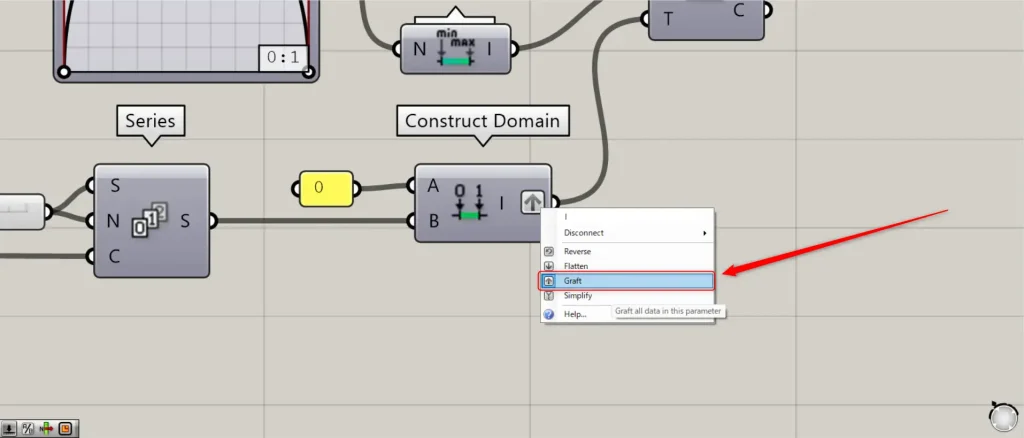
その後、Seriesを、Construct Domain(B)につなげます。
さらに、0の数値を、Construct Domain(A)につなげます。
すると、70個の数値範囲が作成されます。
この際に、Construct Domain(I)を右クリックし、Graftに設定してください。
その後、Graph Mapperを、Remap Numbers(V)につなげます。
さらに、Boundsを、Remap Numbers(S)につなげます。
さらに、Construct Domainを、Remap Numbers(T)につなげます。
すると、Graph Mapperから出力される数値が、新たな数値範囲内に応じて数値が変わりました。
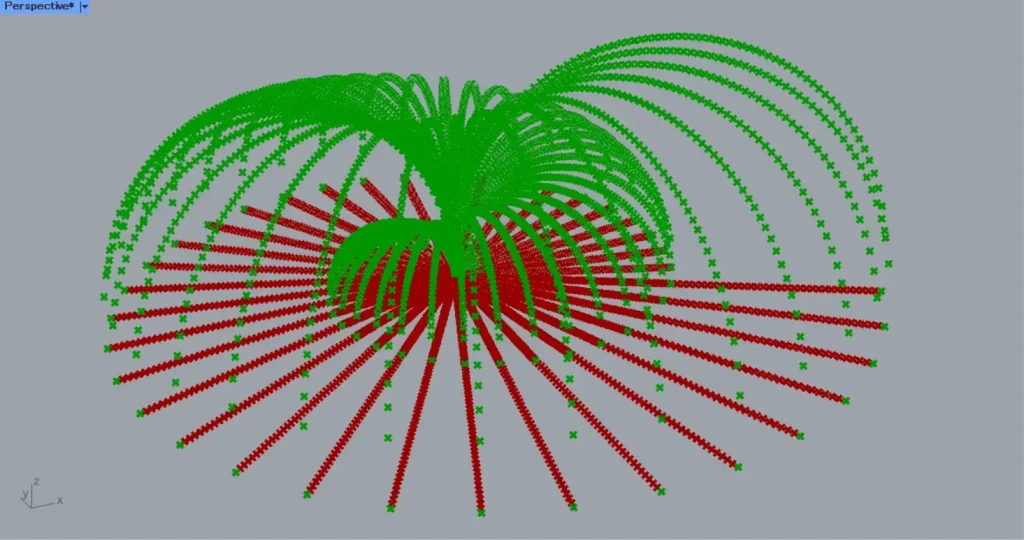
その後、Remap Numbers(R)を、Unit Zにつなげます。
さらに、Divide Curve(P)を、Move(G)につなげます。
すると、上の画像のように、点が弧を描くように移動しました。

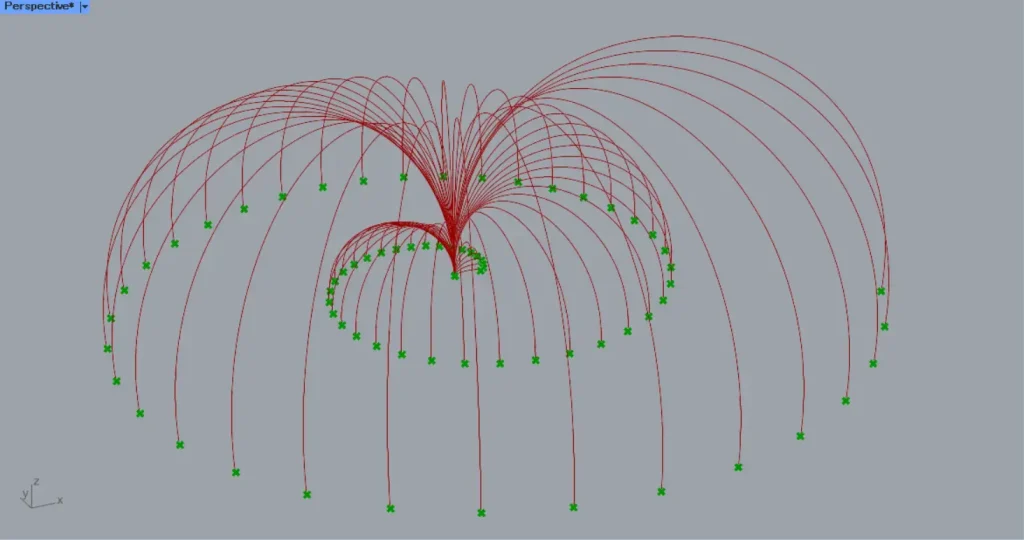
その後、Move(G)を、Interpolate(V)につなげます。
すると、上の画像のように、点をつなぐ曲線が作成されました。
曲線を中心から外側へ移動させる
次に、曲線を中心から外側へ移動させます。
Divide Curve(P)を、2つのList Item(L)につなげます。
1つ目のList item(i)に、0をつなげます。
すると、最初の点を取得できます。
2つ目のList item(i)に、-1をつなげます。
すると、最後の点を取得できます。
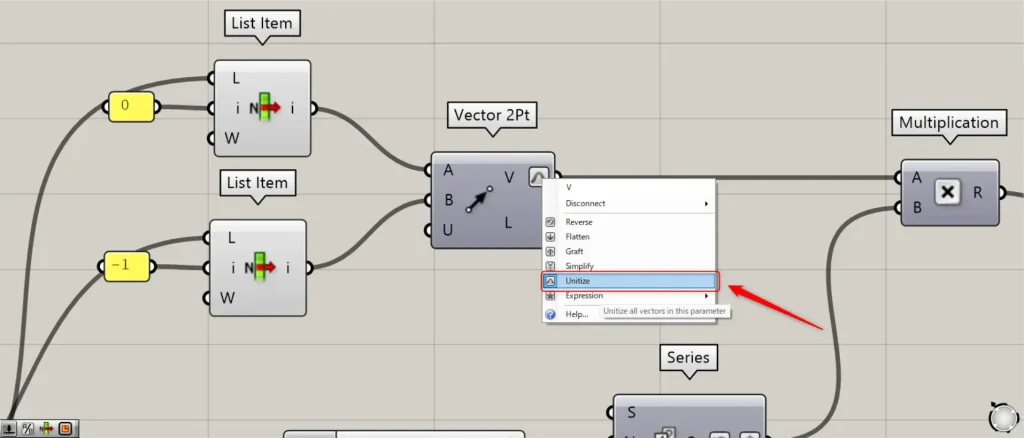
その後、1つ目のList itemを、Vector 2Pt(A)につなげます。
さらに、2つ目のList itemを、Vector 2Pt(B)につなげます。
この際に、Vector 2Pt(V)を右クリックし、Unitizeに設定してください。
すると、1つ目の点から2つ目の点までのベクトルを取得できます。
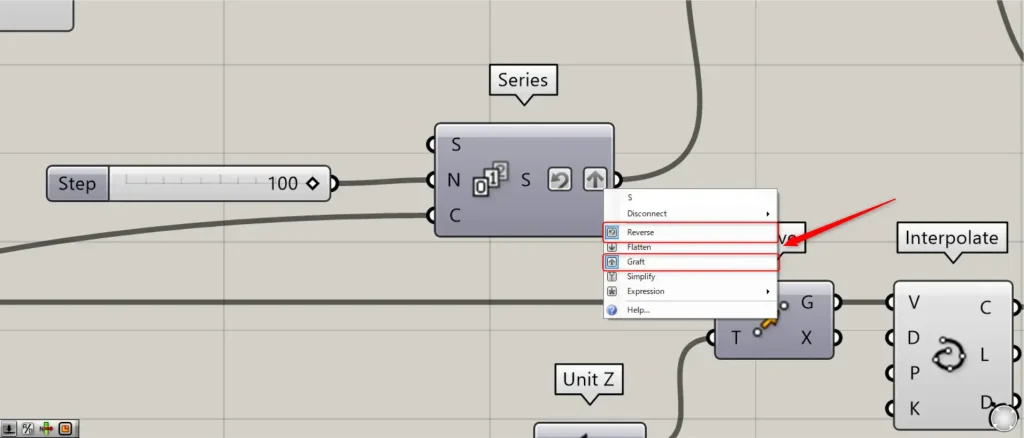
その後、先程の70を、Series(C)につなげます。
さらに、100を、Series(N)につなげます。
この際に、Series(S)を右クリックし、ReverseとGraftに設定してください。
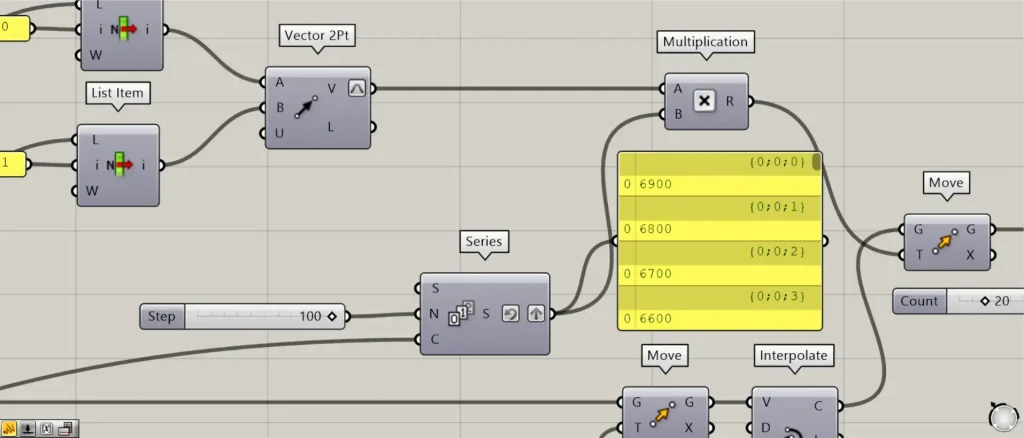
すると、0から100ずつ増加する数値が、70個作成されます。
Reverseに設定してるので、最後の6900から小さくなる順番になってます。

その後、SeriesとVector 2Pt(V)を、Multiplicationにつなげます。
その後、Multiplicationを、Move(T)につなげます。
さらに、Interpolate(C)を、Move(G)につなげます。
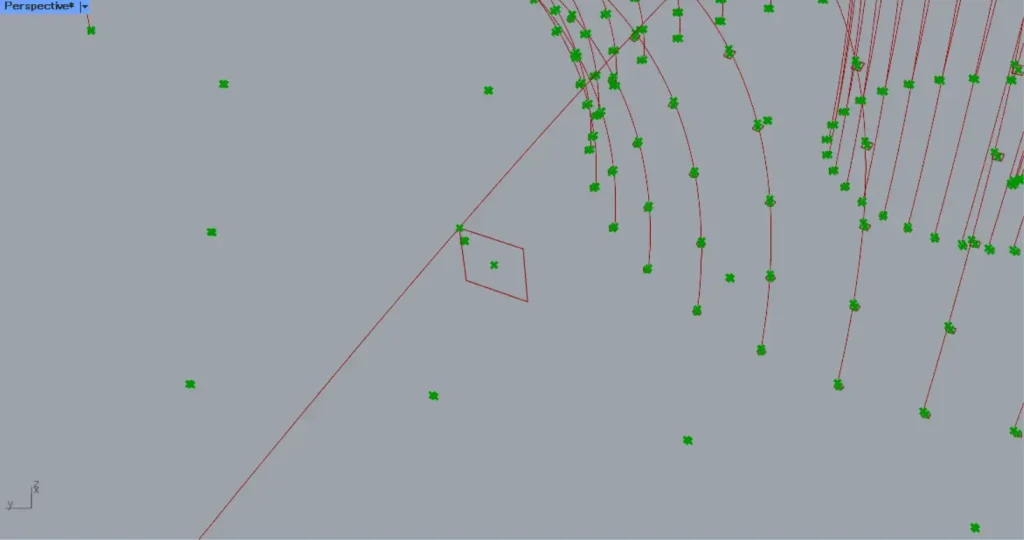
すると、上の画像のように、各曲線が中心から外側に向かって移動します。
これで、線が重ならなくなります。
正方形をつなげるサーフェスを作成する
最後に、正方形をつなげるサーフェスを作成していきます。

Move(G)を、Perp Frames(C)につなげます。
さらに、平面の個数の数値を、Perp Frames(N)につなげます。
今回は、20を入力しています。
すると、各曲線上に、20個の作業平面が作成されます。
その後、Perp Frames(F)を、Rectangle(P)につなげます。
さらに、辺の長さの数値を、Rectangle(XとY)に入力します。
今回は、どちらにも80を入力しています。
すると、上の画像のように、各曲線状に正方形の線が作成されました。
その後、Perp Frames(F)を、Deconstruct Planeにつなげます。
すると、作業平面の原点の点データを取得できます。
すると、四角形の中心点の点データを取得できます。
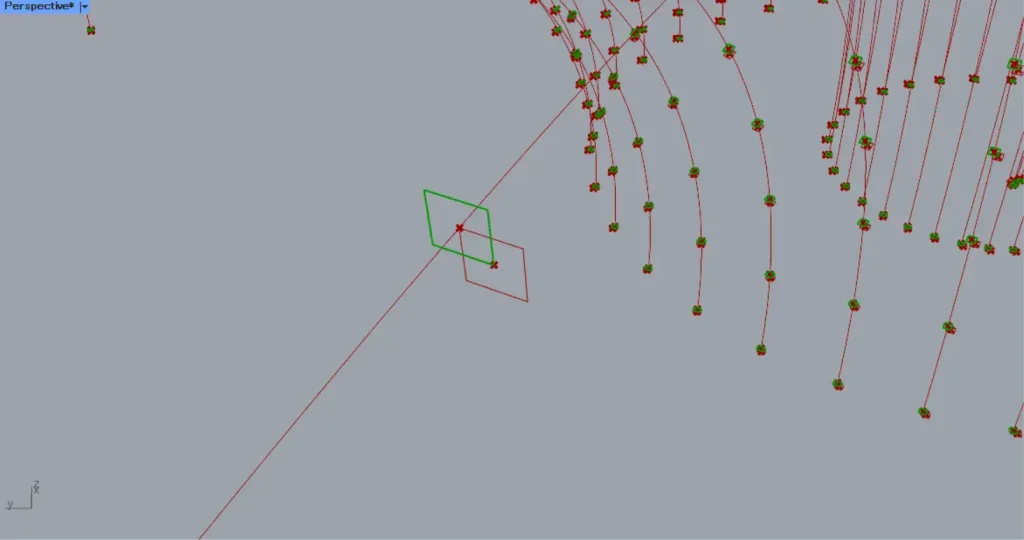
その後、Area(C)を、Vector 2Pt(A)につなげます。
さらに、Deconstruct Plane(O)を、Vector 2Pt(B)につなげます。
すると、正方形の中心点から、作業平面の原点までのベクトルデータを取得できます。
その後、Vector 2Ptの(V)を、Move(T)につなげます。
さらに、Rectangle(R)を、Move(G)につなげます。
すると、上の画像のように、正方形の線が、作業平面の原点を中心にする位置に移動しました。

すると、上の画像のように、四角形の線をつないでサーフェスが作成されました。
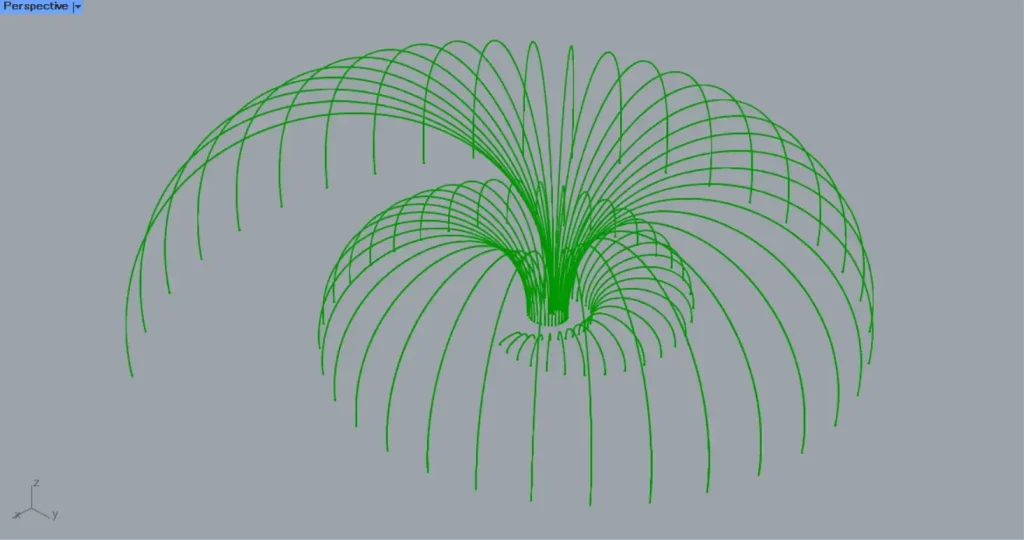
最後に、LoftをCap Holesにつなげ、穴を塞いだら完成です。
今回は以上になります。






Comment