![[Grasshopper]フィボナッチ数列を作成するFibonacciの使い方](https://iarchway.com/wp-content/uploads/2025/06/eyecatch-13.png)
フィボナッチ数列を作成する、Fibonacciの使い方について解説します。
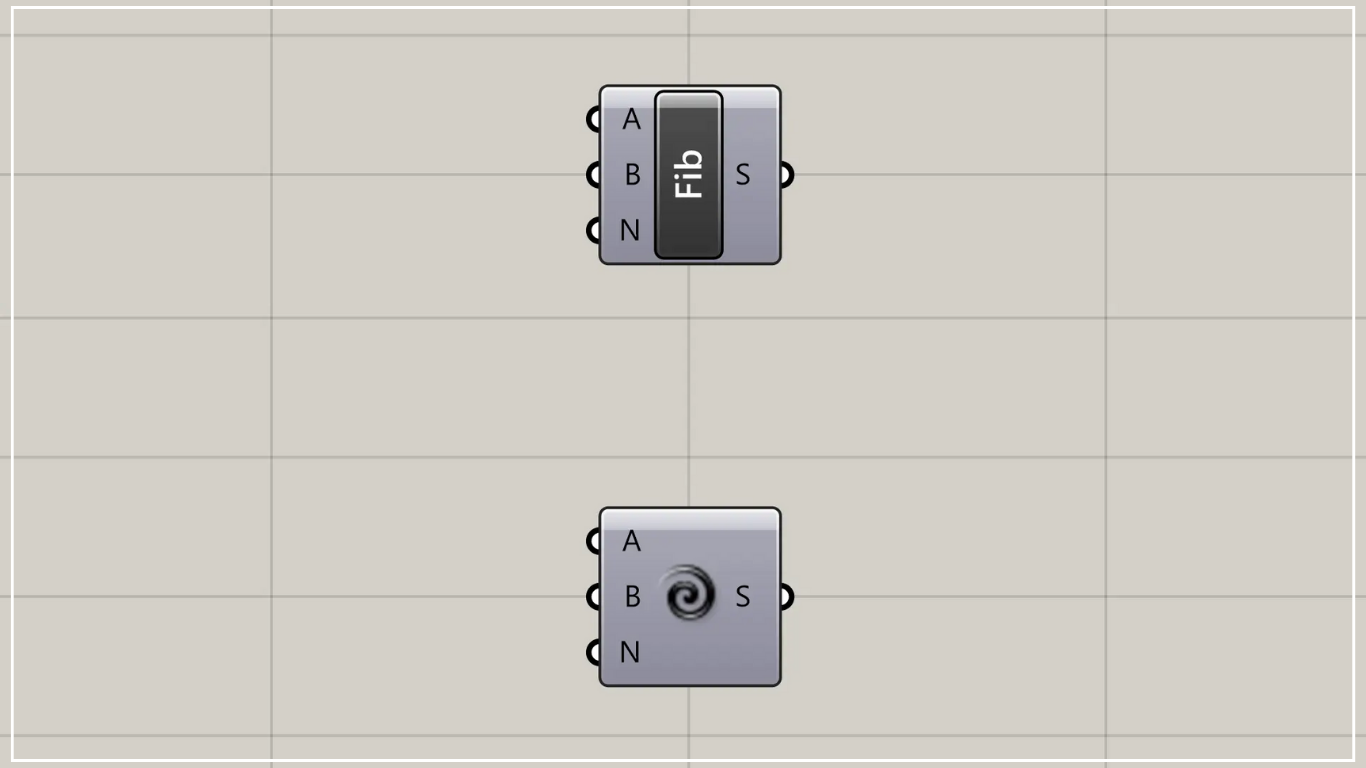
グラスホッパー上では上の２つのどちらかで表されます。
フィボナッチ数列を作成する
Fibonacciを使うことで、フィボナッチ数列を作成することができます。
フィボナッチ数列は、前の2つの数値を足して数値を作成していく数列になります。
Fibonacci(N)には、最初の2つの数値を除いた数値の個数をつなげます。
今回の場合、5をつなげています。
すると、最初の2つの数値である0と1を除くと、5つの数値が作成され、すべて含めると7つの数値が作成されます。
数値を見てみると、1つ目は0、2つ目は1であり、3つ目は0+1=1、4つ目は1+1=2・5つ目は1+2=3という数列になっていることが分かります。
Fibonacci(A)に数値をつなげると、最初の数値を設定できます。
Fibonacci(B)に数値をつなげると、2つ目の数値を設定できます。
使用例
Fibonacciの使用例を見てみましょう。
今回は、フィボナッチ数列を使った曲線を作成してみます。
使用コンポーネント：①Fibonacci ②Point ③Circle ④List Length ⑤Divide Curve ⑥Vector 2Pt ⑦Multiplication ⑧Move ⑨Interpolate ⑩Boolean Toggle
今回は、Fibonacci(N)に10をつなげ、12個の数値を作成しています。
最初に、任意の場所にPointで点を作成します。
さらに、半径の数値を、Circle(R)につなげます。
今回は、150をつなげています。
すると、上の画像のように、円が作成されました。
その後、Fibonacciを、List Lengthにつなげます。
すると、作成した数値の個数の12が出力されます。
その後、List Lengthを、Divide Curve(N)につなげます。
さらに、Circleを、Divide Curve(C)につなげます。
すると、上の画像のように、円を12に分割する位置に、点が作成されました。
その後、Pointを、Vector 2Pt(A)につなげます。
さらに、Divide Curve(P)を、Vector 2Pt(B)につなげます。
さらに、Trueの情報を、Vector 2Pt(U)につなげます。
今回は、Boolean ToggleでTrueの情報を作成しています。
すると、円の中心から各分割点へのベクトルデータが作成されます。
その後、FibonacciとVector 2Pt(V)を、Multiplicationにつなげます。
すると、作成した数値に、ベクトルを合わせることができます。
その後、Multiplicationを、Move(T)につなげます。
すると、上の画像のように、円の中心点が移動しました。
その後、Move(G)を、Interpolate(V)につなげます。
すると、上の画像のように、点をつなぐ曲線が作成されました。
これでフィボナッチ数列を使った曲線の完成です。
自然界に存在するフィボナッチ数列を使うことで、上の記事のような木なども作成することができます。
Fibonacciコンポーネントを使用しているグラスホッパー記事はこちら↓
Comment