![[Grasshopper]Divide Surfaceコンポーネントの使い方](https://iarchway.com/wp-content/uploads/2024/03/eyecatch-2.png)
Divide Surfaceコンポーネントの使い方について解説します。
グラスホッパー上では上の２つのどちらかで表されます。
サーフェスを点で分割する
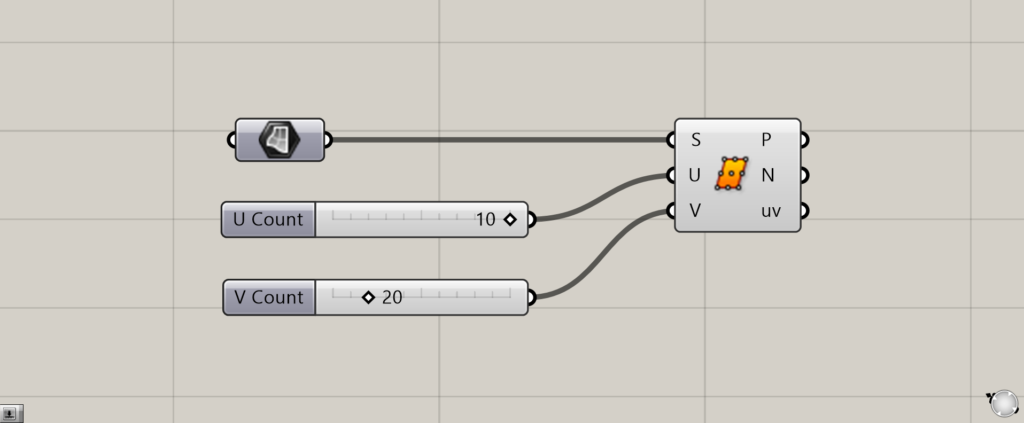
基本的な全体コンポーネントは上の画像のようになります。
今回は、Surfaceにサーフェスを格納しています。
S端子にはサーフェス、U・V端子には2つの方向の分割する数値を入力します。
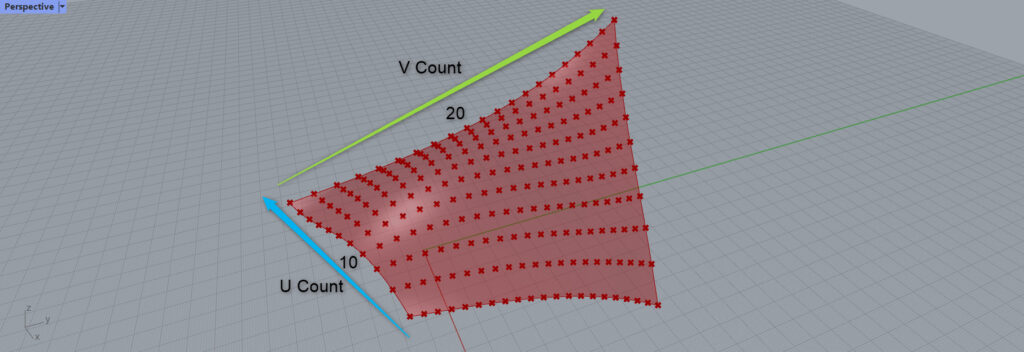
すると、このようにサーフェスが点で分割されています。
U端子に10、V端子に20の数値を入力したので、このように10×20で分割されました。
点を取得する
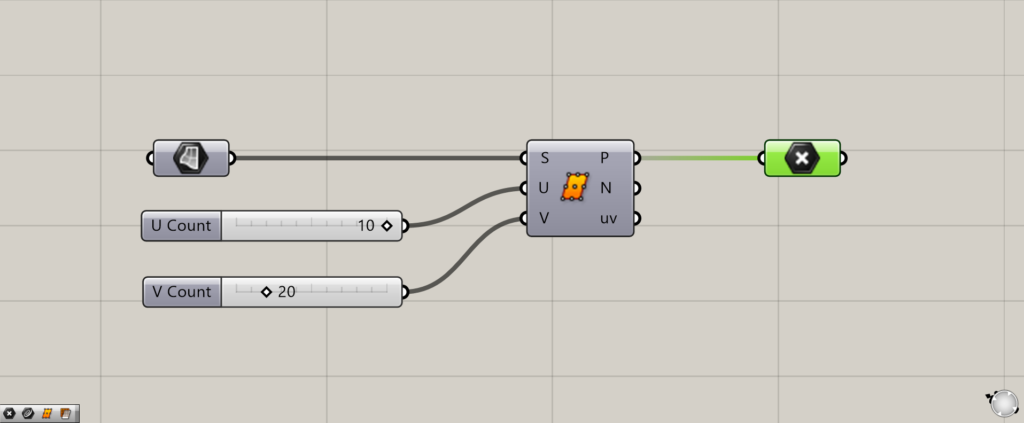
サーフェスを分割する点は、P端子から出力されます。
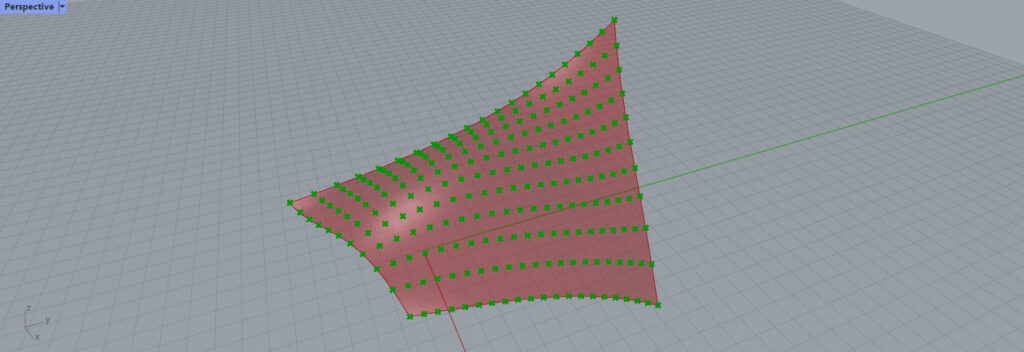
このように、点を取得することができました。
法線ベクトルを取得する
N端子からは、法線ベクトルを取得することができます。
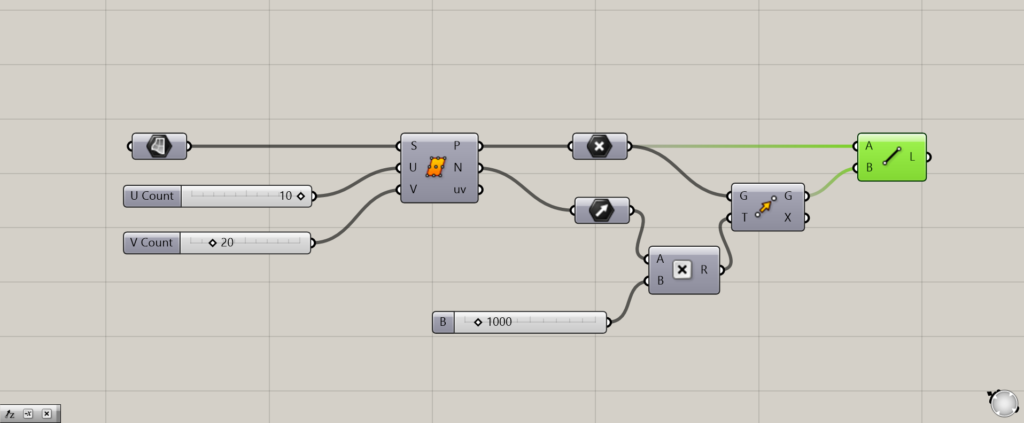
今回は法線ベクトルを分かりやすくするため、上のようなプログラムを作りました。
サーフェスを分割する点を、法線ベクトルの方向にMoveで移動させます。
その後、移動前と移動後の点をLineを使い、線で結びました。
法線ベクトルと数値を掛け算するMultiplicationで掛け合わせると、その方向に移動する距離を決められます。
すると、それぞれの法線ベクトルの方向に線が伸びていることが分かります。
UV値を取得する
UV値を取得します。
UV値は簡単に言うと、複雑な形態のサーフェスなどを分割する際、単純化したもので考えるということです。
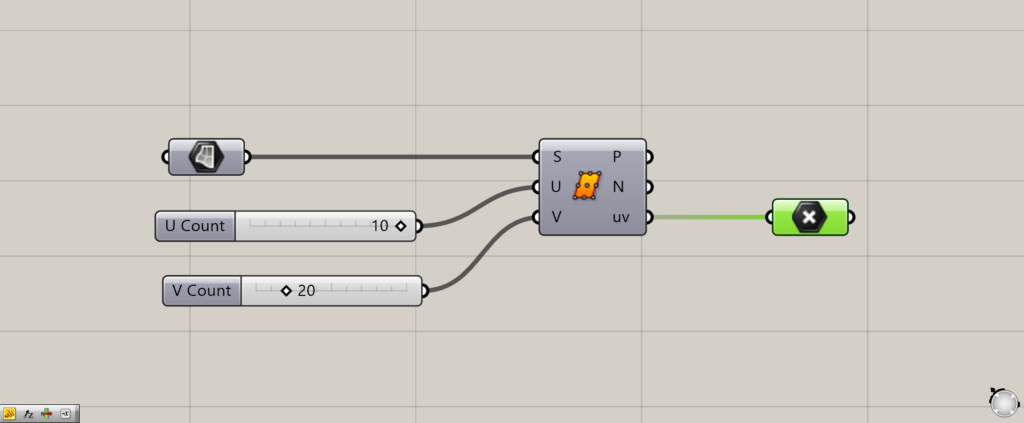
UV端子にPointコンポーネントで点を取得します。
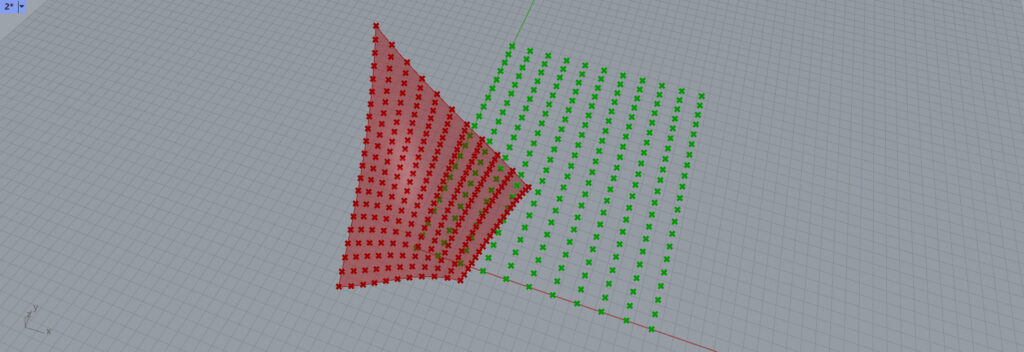
すると、原点を起点にこのようにきれいに配列した点が出現しました。
一見、元々のサーフェスの分割は複雑に見えますが、この緑の点でできた四角形が、この複雑のサーフェスに適応させるのなら、それぞれの点がどのあたりに来るのだろうというのが、UVの考え方になります。
Divide Surfaceコンポーネントを使用しているグラスホッパー記事はこちら↓
Comment