[Grasshopper]平面上の近くの点をつなぐ直線を作成するProximity 2Dの使い方

平面上の近くの点をつなぐ直線を作成する、Proximity 2Dの使い方について解説します。

グラスホッパー上では上の２つのどちらかで表されます。

平面上の近くの点をつなぐ直線を作成する

Proximity 2Dを使うことで、平面上の近くの点をつなぐ直線を作成することができます。

今回の例として、上の画像の複数の点を使います。

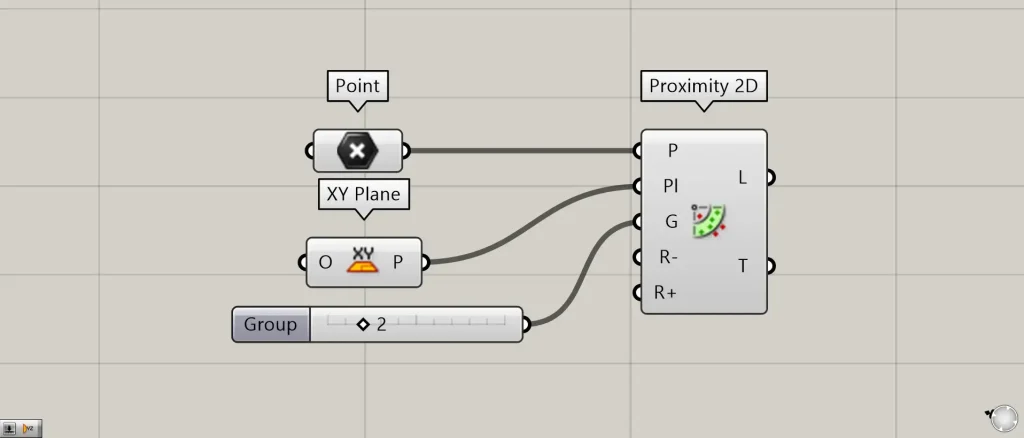
使用コンポーネント：①Point ②XY Plane ③Proximity 2D

今回は、Pointに複数の点を格納しています。

点データが入っているPointを、Proximity 2D(P)につなげます。

また、今回は点がXY平面上にあるので、XY Planeを、Proximity 2D(Pl)につなげます。

さらに、各点から、いくつの周辺の点をつなぐ直線を作成するかの数値を、Proximity 2D(G)につなげます。

最初は、2をつなげています。

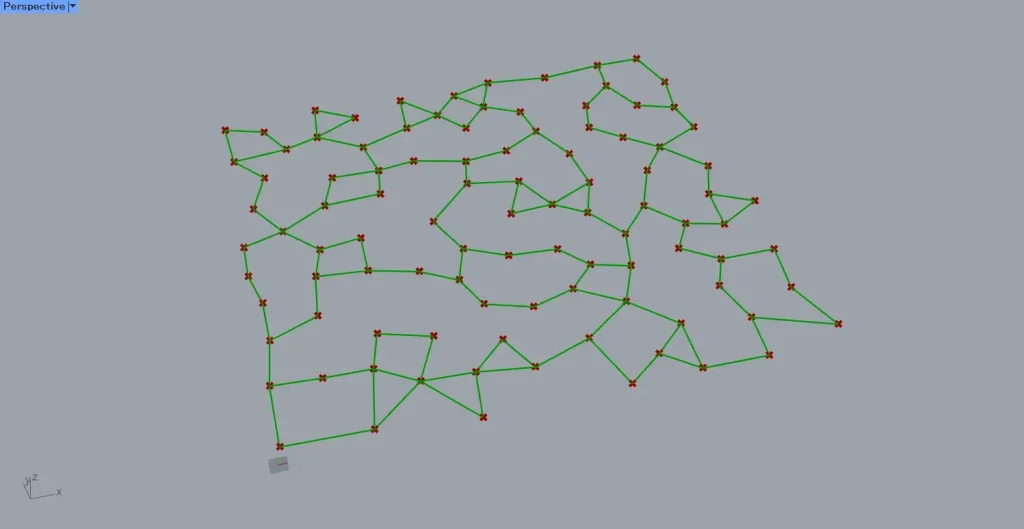
すると、上の画像のように、各点から近くの2つの点をつなぐ直線が作成されました。

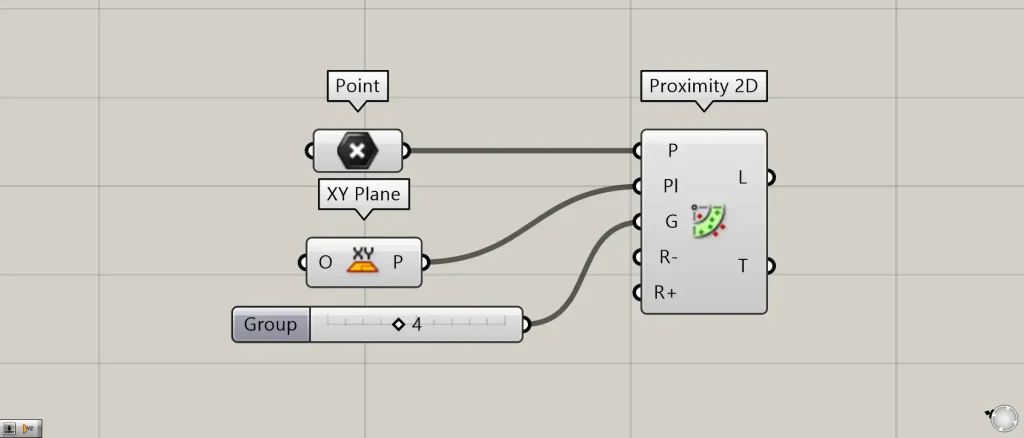
Proximity 2D(G)につなぐ数値を、2から4に変更してみます。

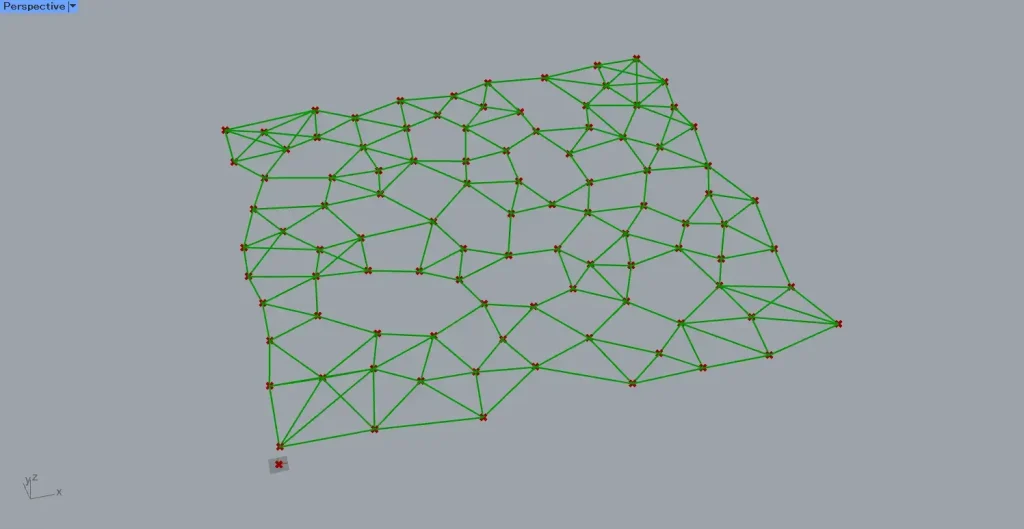
すると、上の画像のように、直線の本数が増えたことが分かります。

このように、Proximity 2Dで、平面上の近くの点をつなぐ直線を作成することができます。

直線が作成される範囲を指定する

半径を指定することで、直線が作成される範囲を指定することもできます。

追加コンポーネント：①List Item ②Sphere

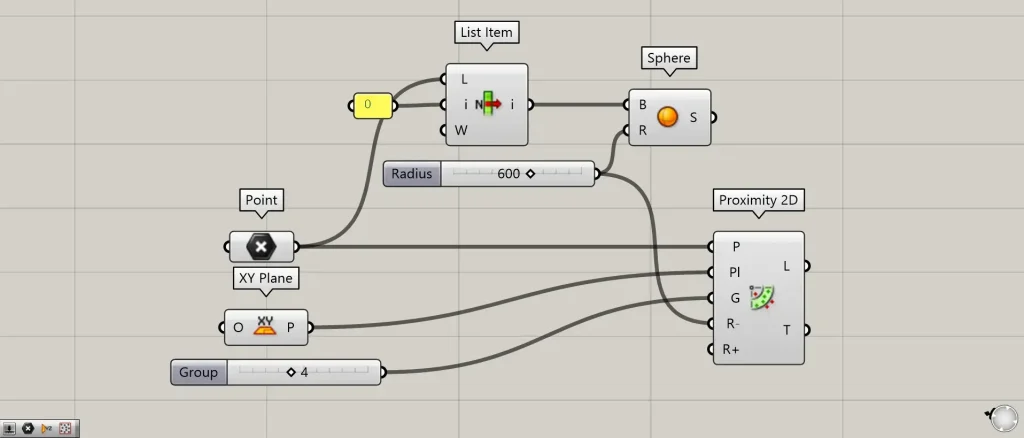
例として、1つの点を取得し、その点を中心とする球を作成して見てみます。

Pointを、List Item(L)につなげます。

今回は1番最初の点を取得するため、0をList Item(i)につなげます。

すると、1つの点を取得できます。

その後、List Itemを、Sphere(B)につなげます。

さらに、半径の数値を、Sphere(R)につなげます。

今回は、600をつなげています。

すると、取得した点を中心とする、半径600の球が作成されます。

先程使用した、半径の600を、Proximity 2D(R-)につなげます。

すると、上の画像のように、直線が指定した半径内には作成されません。

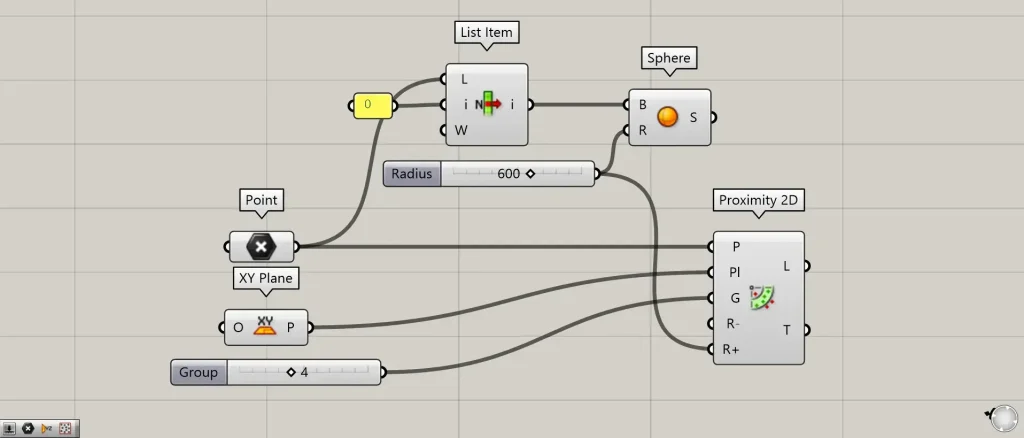
今度は、半径の600を、Proximity 2D(R+)につなげます。

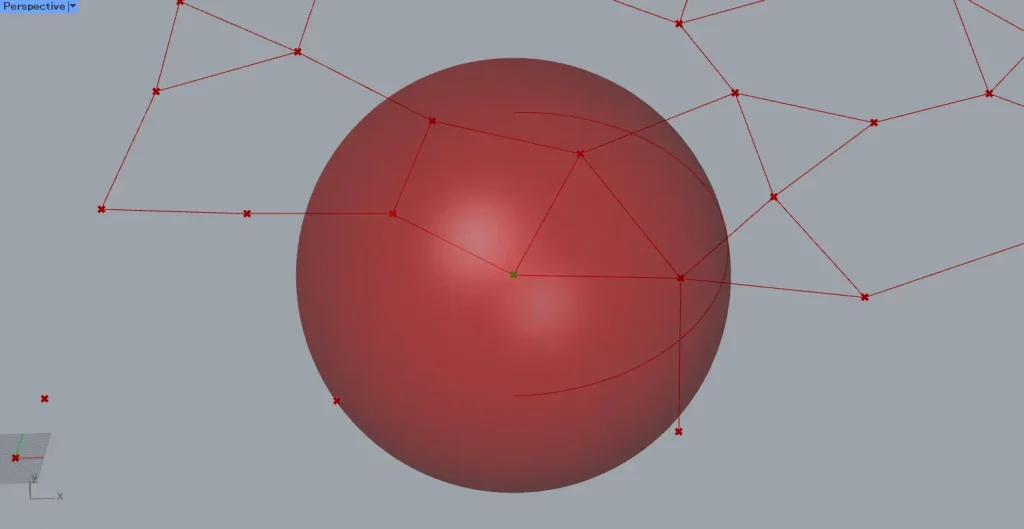
すると、上の画像のように、直線が指定した半径内にのみ作成されます。

このように、半径を指定することで、直線が作成される範囲を指定することもできます。

出力されるデータ

出力されるデータを見てみます。

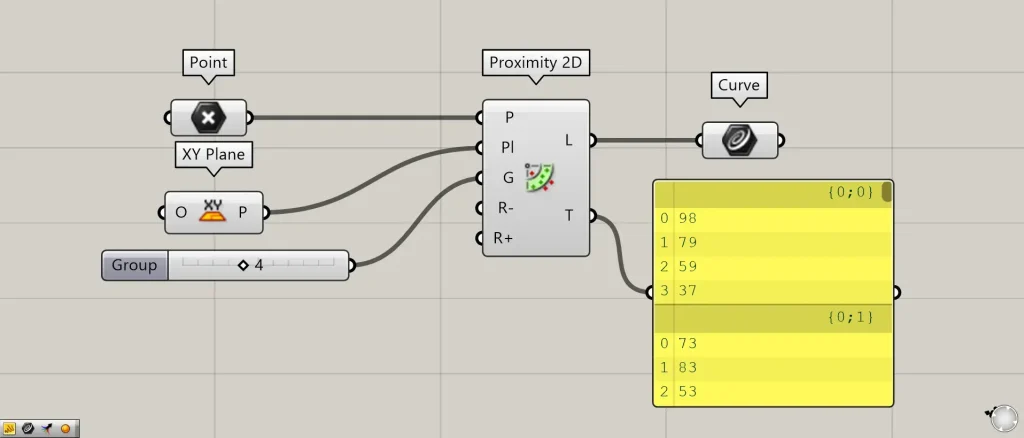
追加コンポーネント：①Curve

Proximity 2D(L)からは、作成された直線の線データが出力されます。

Proximity 2D(T)からは、各点をつなぐ点のインデックス番号（順番の番号）が出力されます。

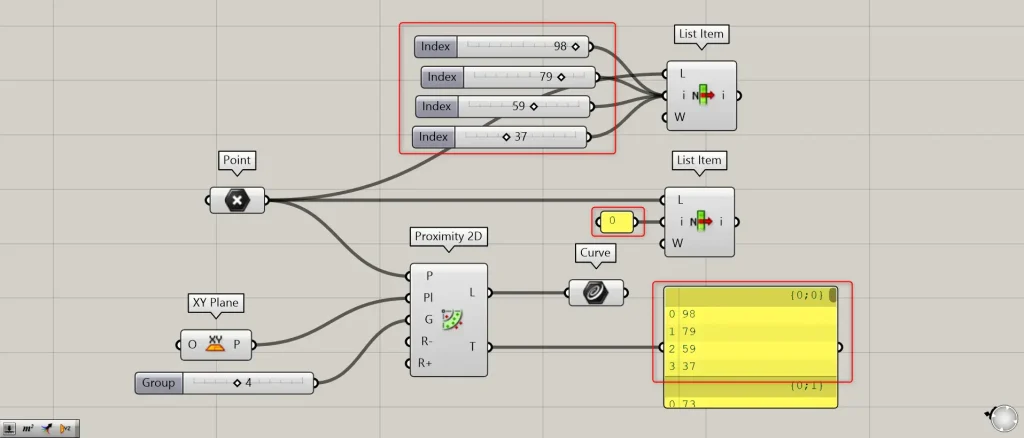
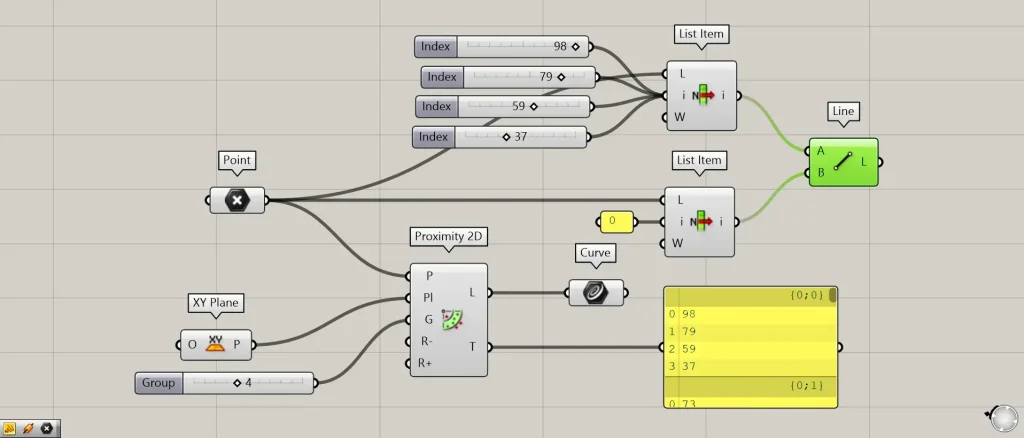
例として、Proximity 2D(T)の1つ目の階層の{0;0}の数値を見てみます。

1つ目の点を取得するため、PointをList Item(L)につなぎ、0をList Item(i)につなげます。

さらに、1つ目の階層内の数値のを、もう1つのList Item(i)につなげます。

今回の場合、98・79・59・37をつなげています。

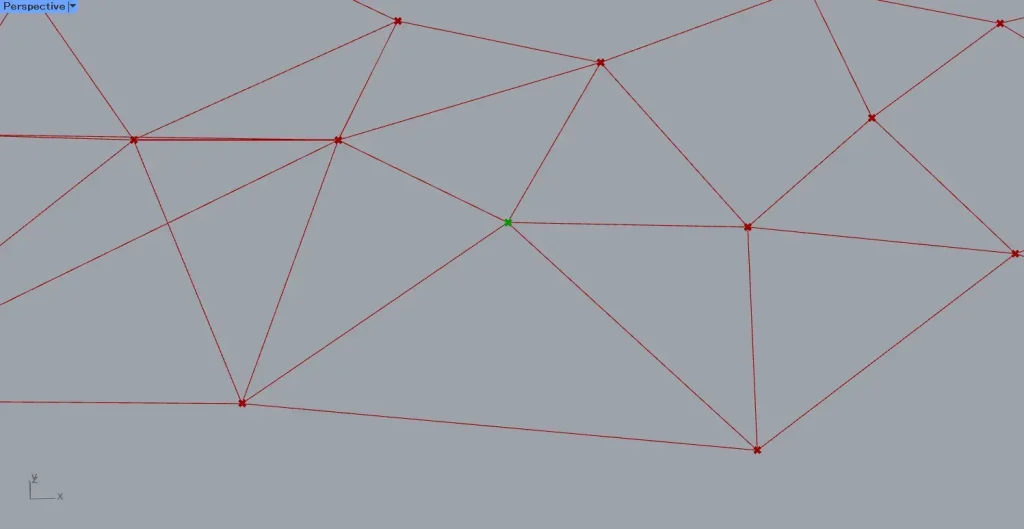
上の画像は、0をList Item(i)につないで取得した1つの点です。

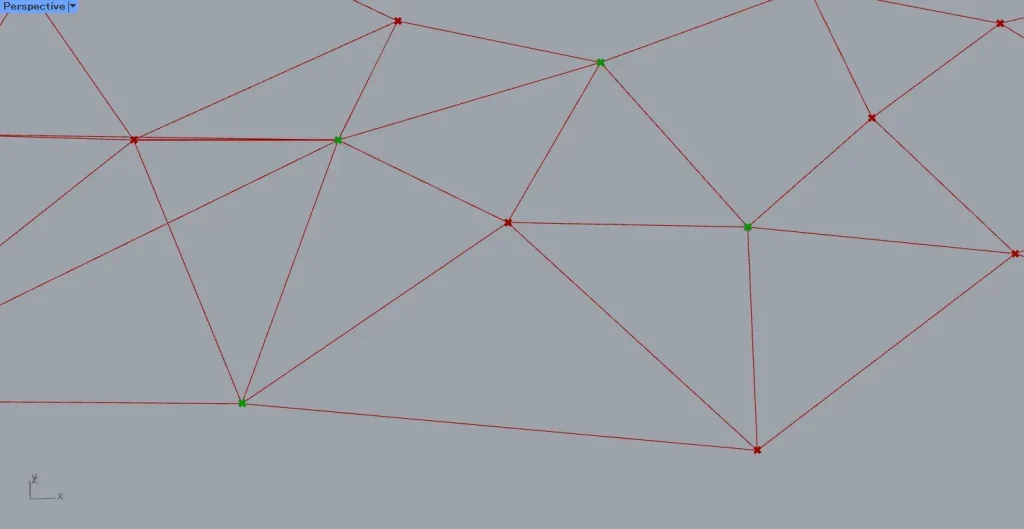
上の画像は、1つ目の階層内の数値の98・79・59・37を、List Item(i)につないで取得した4つの点です。

追加コンポーネント：①Line

取得した点を可視化してみます。

2つのList Itemを、Lineにつなげます。

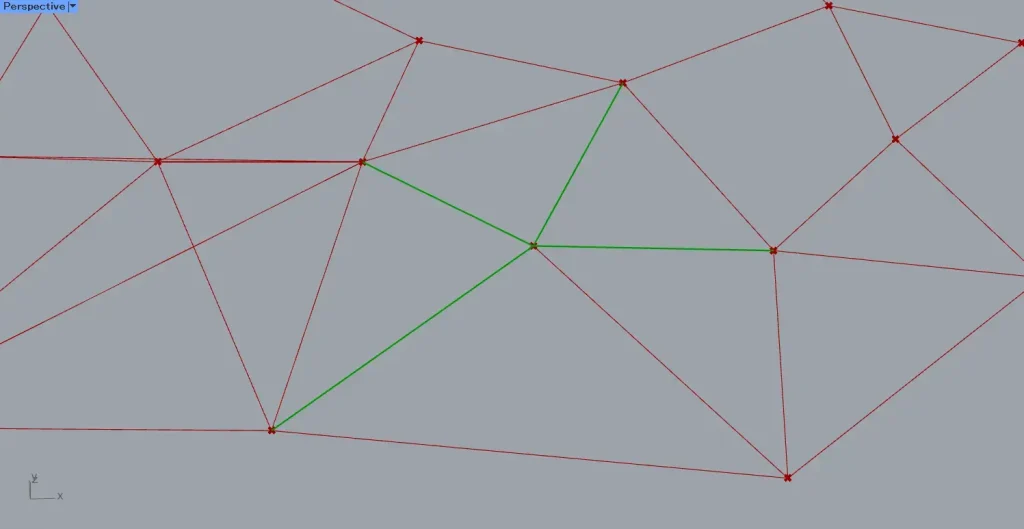
すると、上の画像のように、直線が可視化されました。

このように、Proximity 2D(T)からは、各点が取得した周辺の点の、インデックス番号が出力されます。

Proximity 2Dコンポーネントを使用しているグラスホッパー記事はこちら↓