[Grasshopper]Evaluate Surfaceコンポーネントの使い方

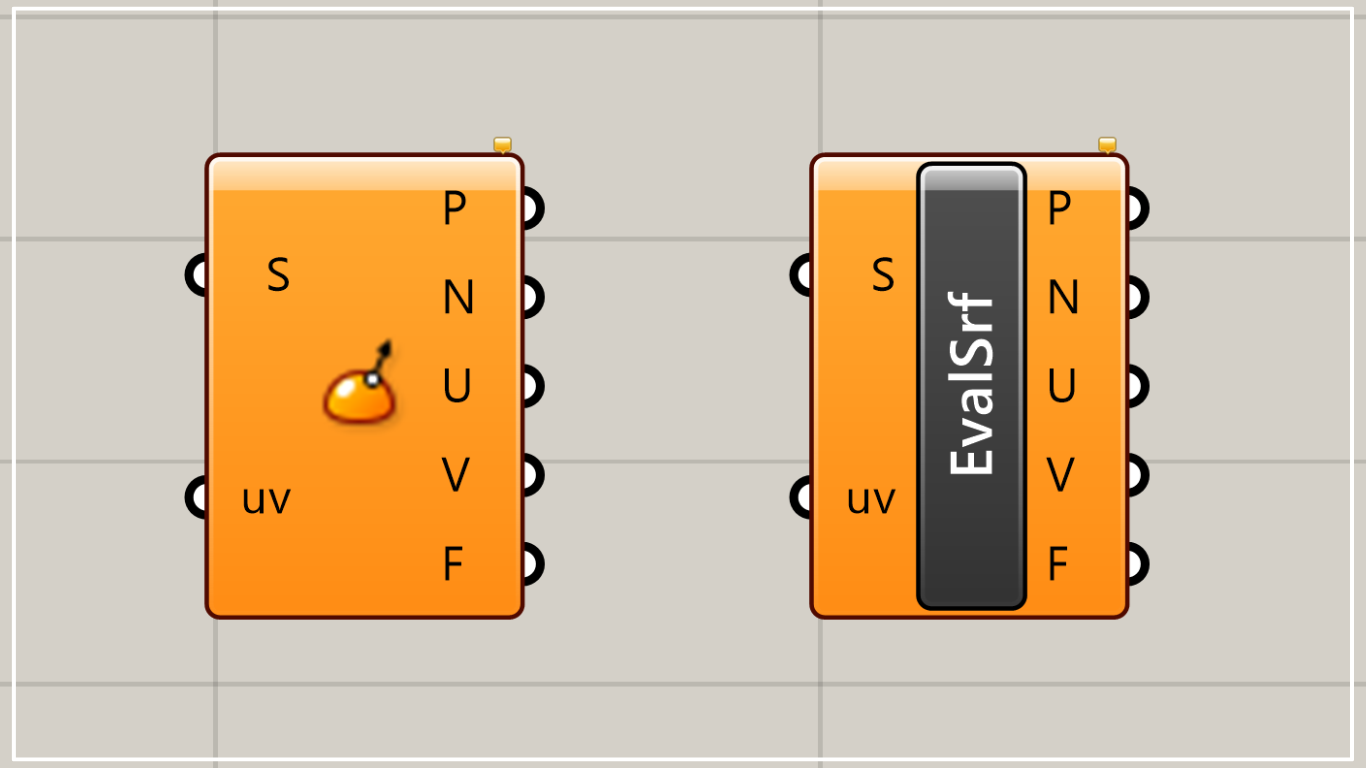
Evaluate Surfaceコンポーネントの使い方について解説します。

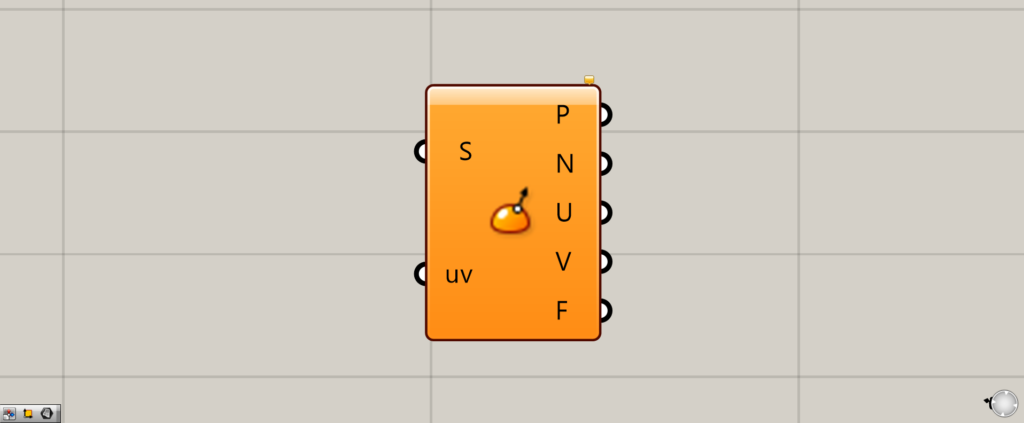
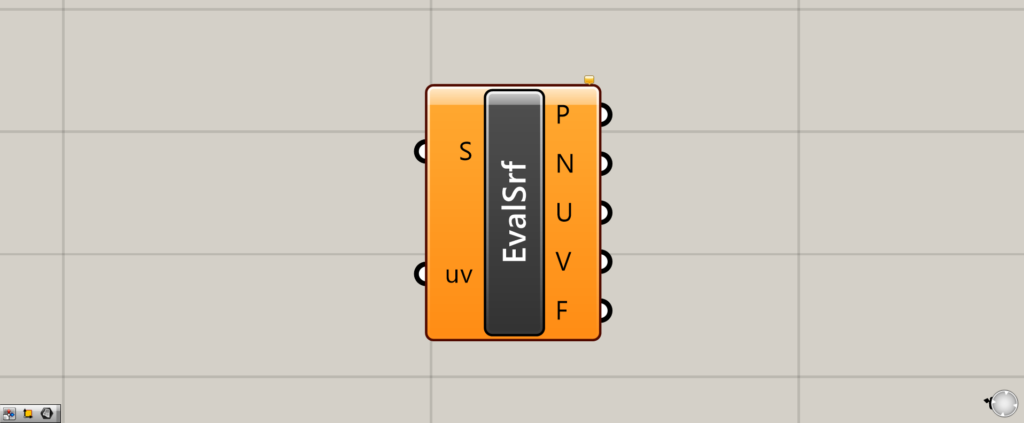
グラスホッパー上では上の２つのどちらかで表されます。

Evaluate Surfaceの基本

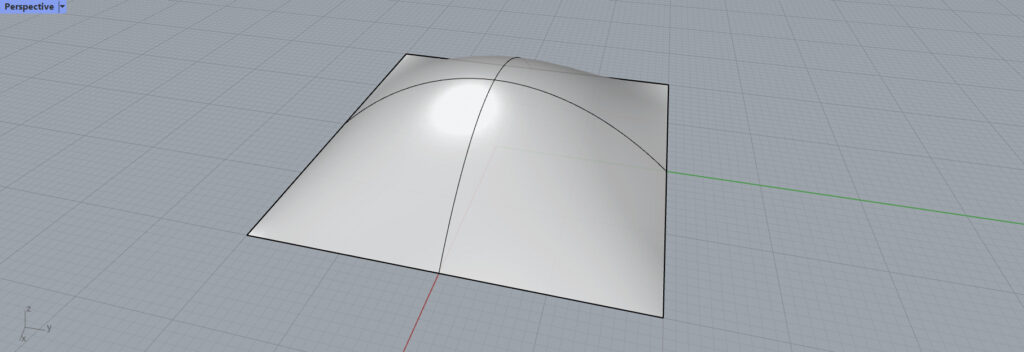
今回はこのサーフェスを使用して、Evaluate Surfaceの使い方を解説します。

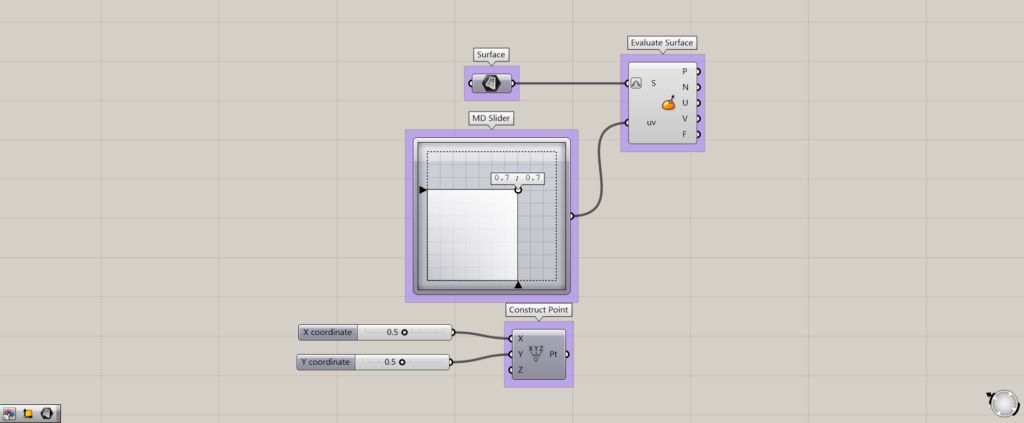
使用コンポーネント：①Surface ②Evaluate Surface ③MD Slider ④Construct Point

こちらが基本的なEvaluate Surfaceの全体コンポーネントになります。

Reparameterizeに設定

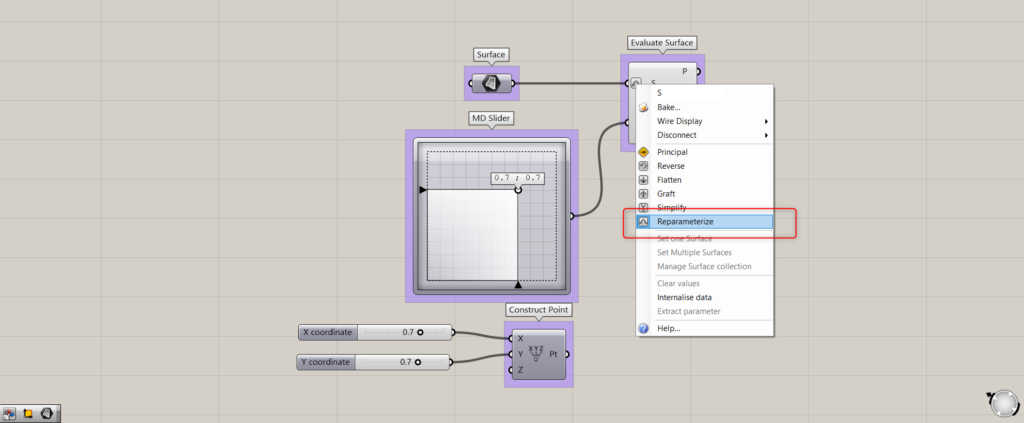
下準備として、Evaluate SurfaceのS端子を右クリックし、Reparameterizeに設定してください。

これは、サーフェス上の位置などの操作をする際に、0~1の値でサーフェスの位置を表すことができるようになるからです。

例えば、横幅が1000mmのサーフェスの中心である500の位置を、0.5として表せるようになります。

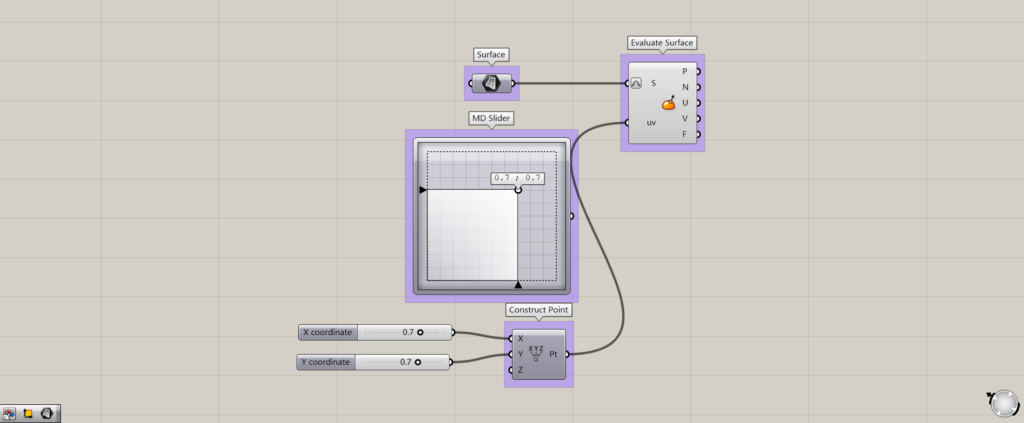
MD SliderとConstruct Point

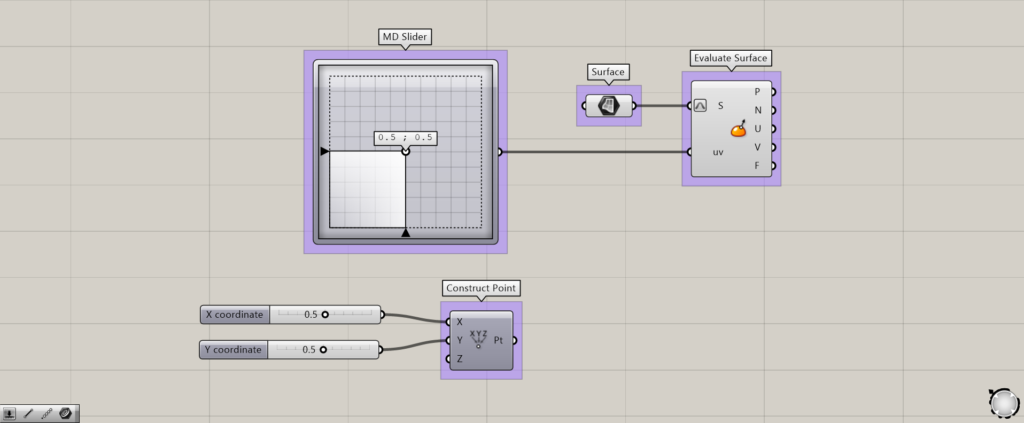
MD SliderとConstruct Pointの説明です。

これらの数値を0~0.1で動かすことにより、サーフェス上の位置を取得することができるようになります。

使用するサーフェスをS端子に、MD Slider、もしくはConstruct Pointをuvにつなげます。

Construct Pointを使用する際は、XとY端子に0~1.0を設定してください。

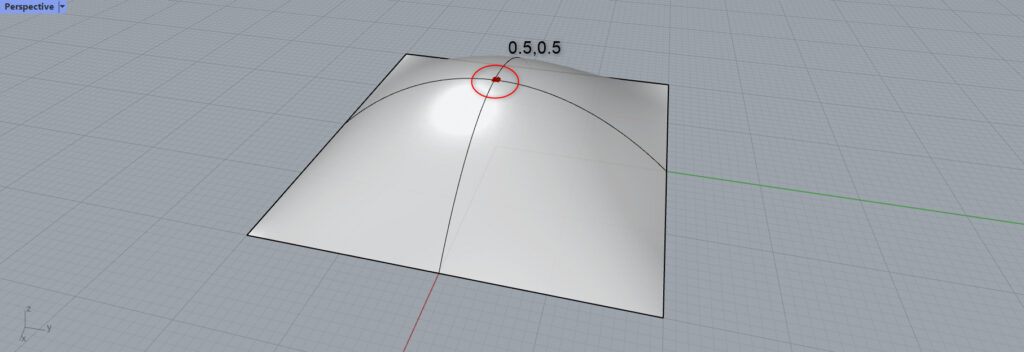
数値が0.5,0.5の位置だと、サーフェスの中心に赤いマークが来ます。

今度は数値を0.7,0.7に変更してみます。

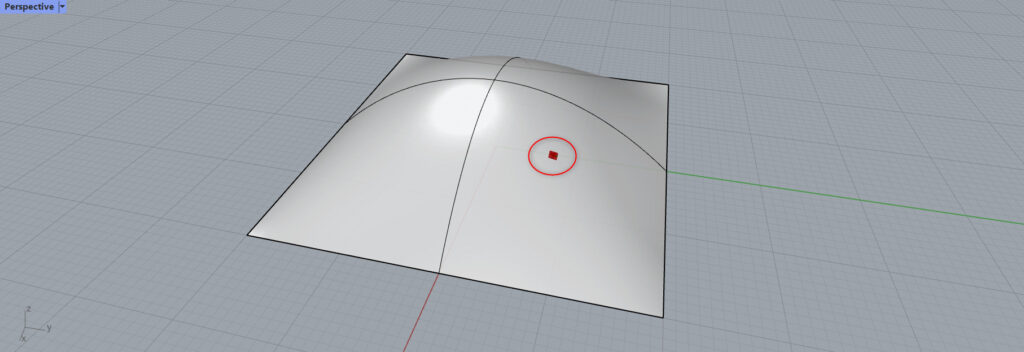
すると、赤いマークは違う場所へ移動しました。

この場所が、このサーフェスの0.7,0.7の位置になります。

MD Sliderではなく、Construct Pointでも同様の結果になります。

Evaluate Surfaceから出力される情報

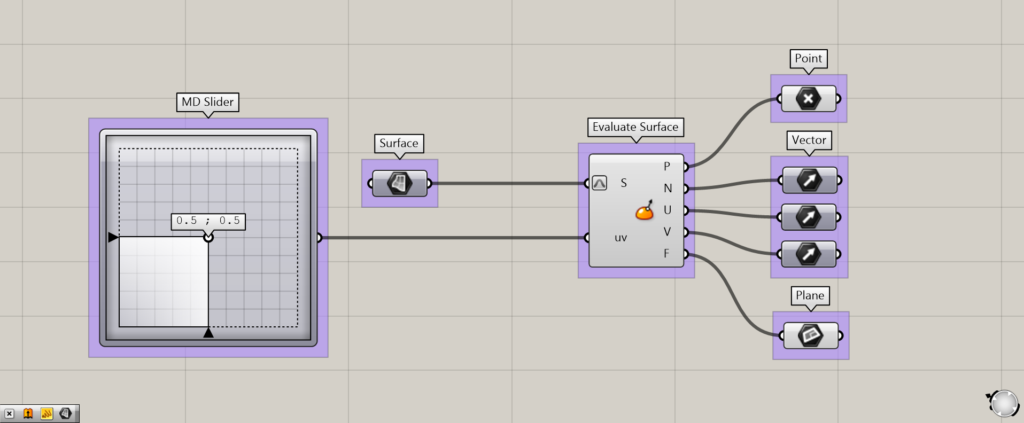
使用コンポーネント：①MD Slider ②Surface ③Evaluate Surface ④Point ⑤Vector ⑥Plane

Evaluate Surfaceから出力される情報は大きく分けて3つあります。

それは、点情報・ベクトル情報・作業平面情報の３つになります。

点情報

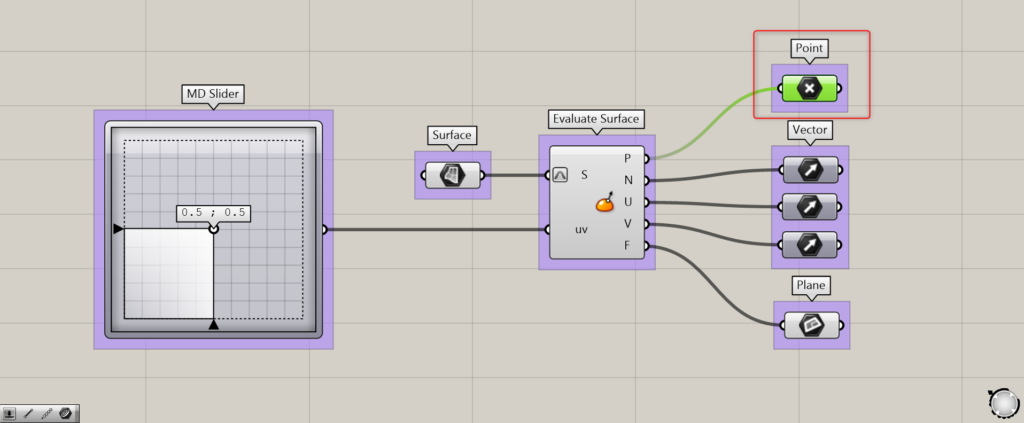
P端子からは、MD SliderやConstruct Pointで指定した位置に点が作成されます。

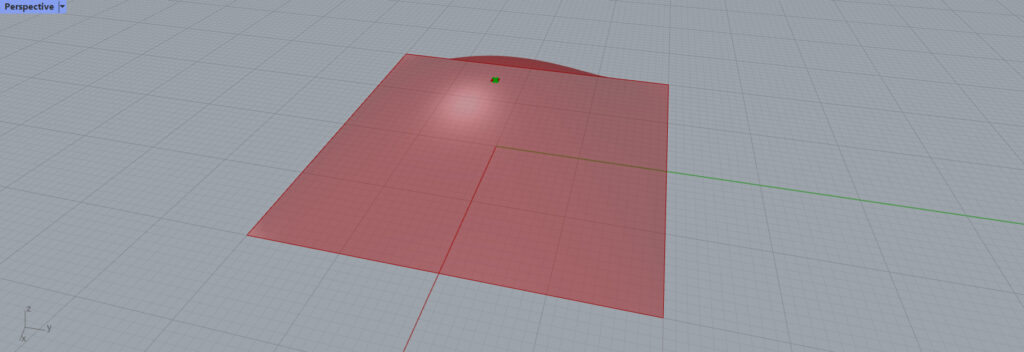
このように、点が作成されることが分かります。

ベクトル情報

Evaluate Surfaceから出力されるベクトル情報は、3つあります。

法線ベクトル（Normal）

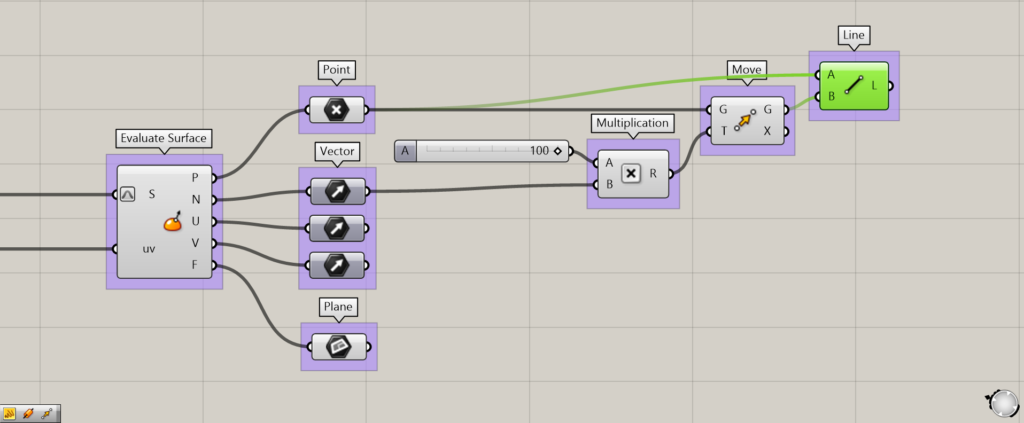
追加コンポーネント：①Multiplication ②Move ③Line

1つ目は、N端子から出力される法線ベクトル（Normal）です。

法線とは、ある直線と垂直に交わる直線です。

曲線においては、曲線上のある点における接線に垂直な直線のことを指します。

法線とは？法線の方程式や法線ベクトルの公式・求め方 | 受験辞典 (univ-juken.com)

今回の場合、サーフェス上の1点から垂直な方向へのベクトルということで理解しても大丈夫です。

今回は法線ベクトルを確認するために、先ほど作成された点をN端子の法線ベクトルで移動し、線を作成しました。

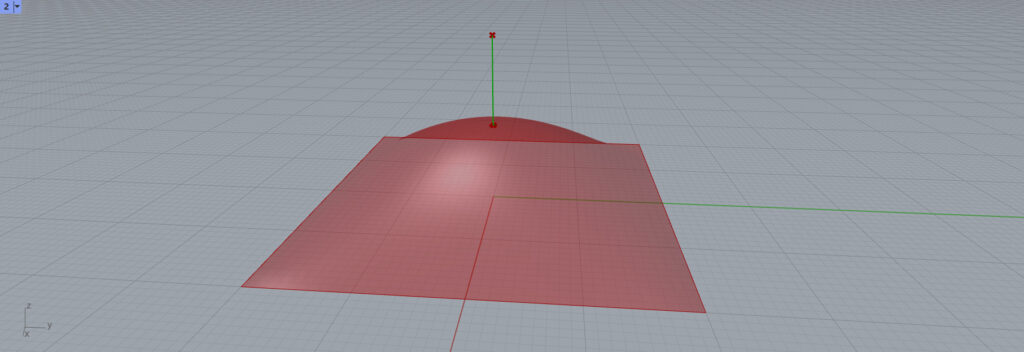
法線ベクトルを使用すると、法線ベクトルの方向へ線が伸びました。

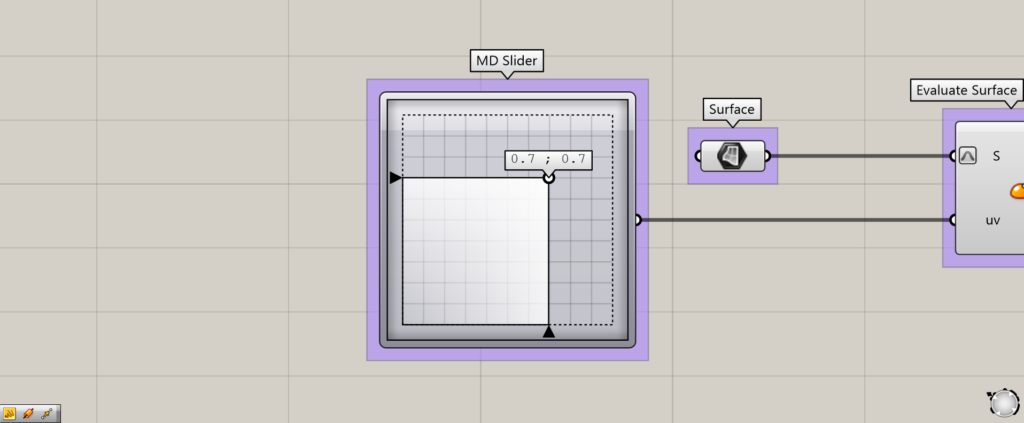
サーフェス上の位置情報を、0.7,0.7に変更してみました。

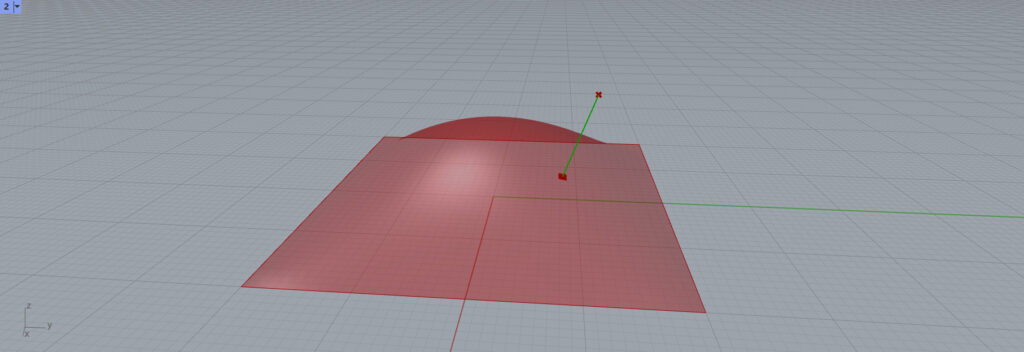
0.7,0.7の位置では、このように伸びました。

UVベクトル

残る2つのベクトルは、UとVベクトルです。

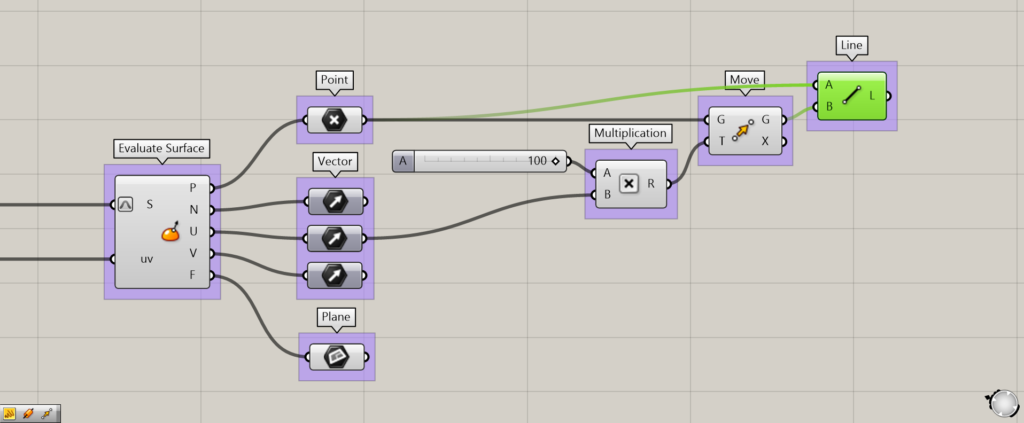
まずはUベクトルから見てみましょう。

先程の線を作成するプログラムのベクトルを、Uベクトルにします。

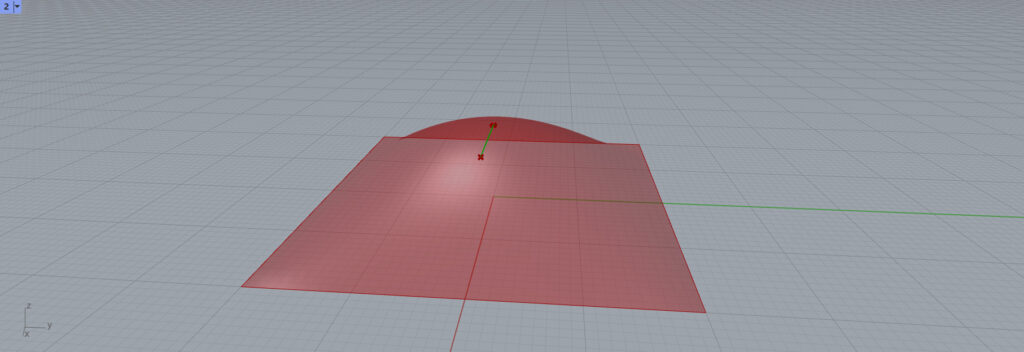
すると、今度は水平方向に線が伸びました。

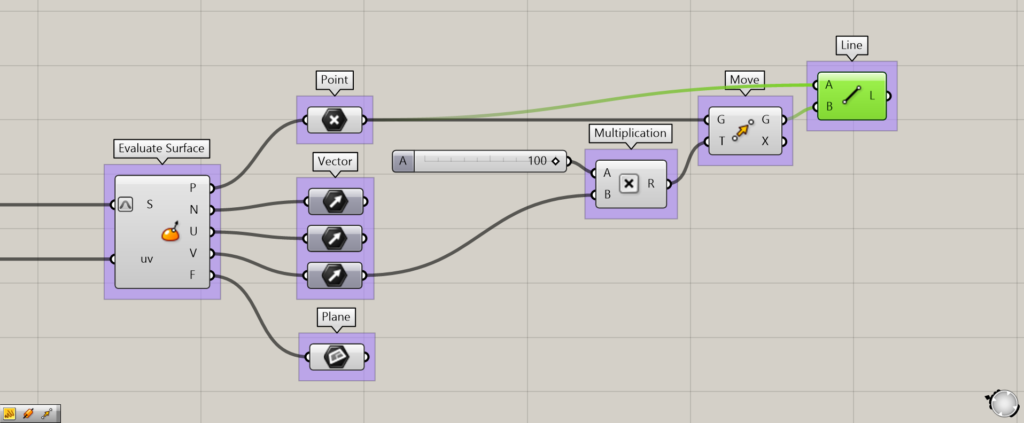
今度はVベクトルで実行します。

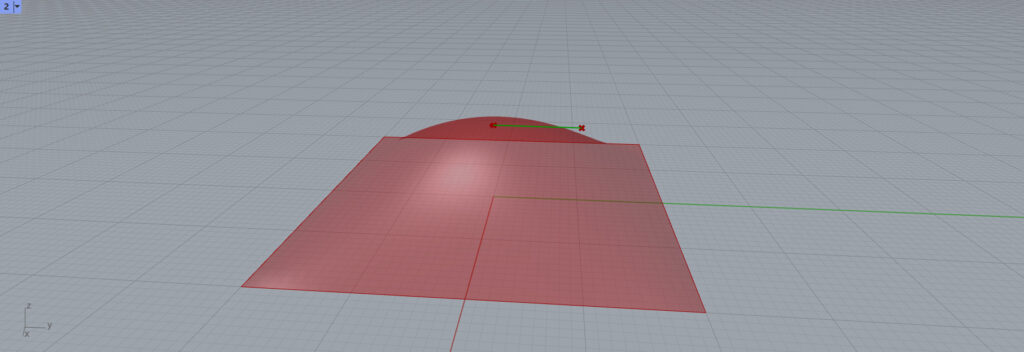
すると、今度は別の水平方向に線が伸びました。

このように、UVベクトルは、サーフェス上の1点の水平方向のベクトルのことです。

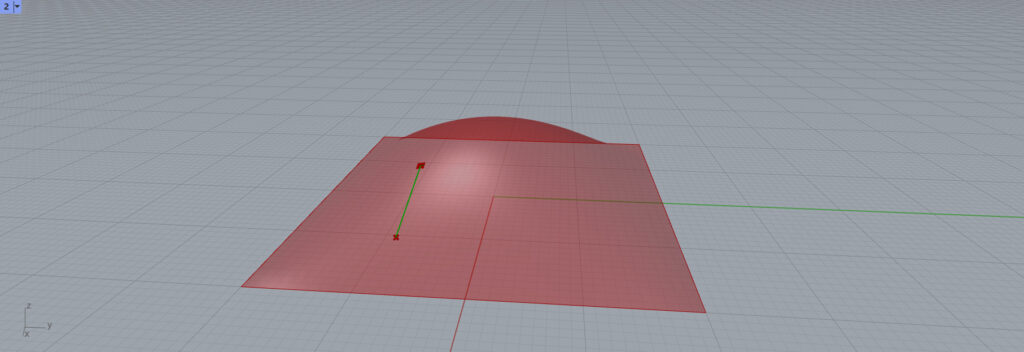
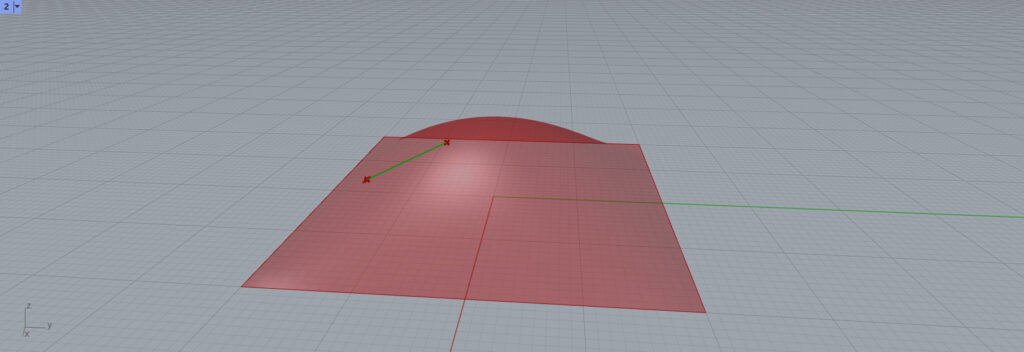
他の位置の場合、このようなサーフェスに水平な線ができました。

作業平面情報

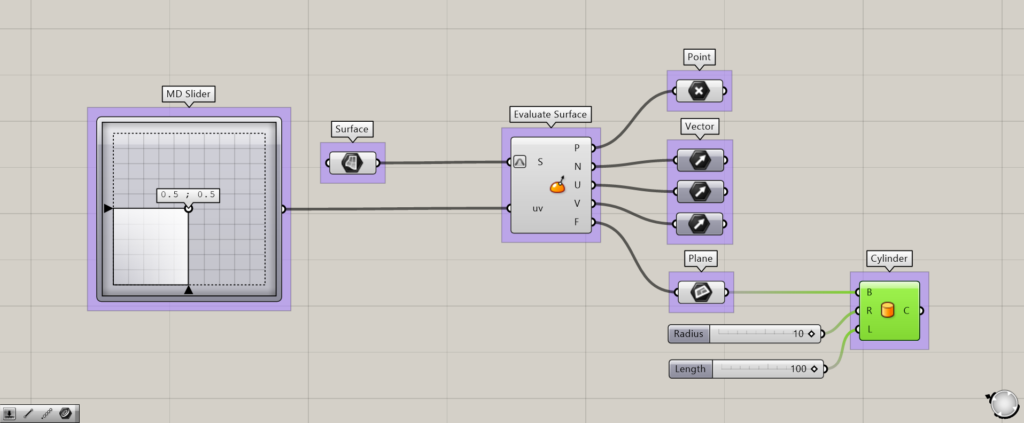
追加コンポーネント：①Cylinder

最後は作業平面についてです。

Evaluate SurfaceのF端子から抽出されます。

これは、サーフェス上のある1点の作業平面を表します。

簡単に言うと、先程の法線ベクトルとUVベクトルが融合した形だと思ってください。

今回は、Cylinderと作業平面を使用し、円柱を作成してみます。

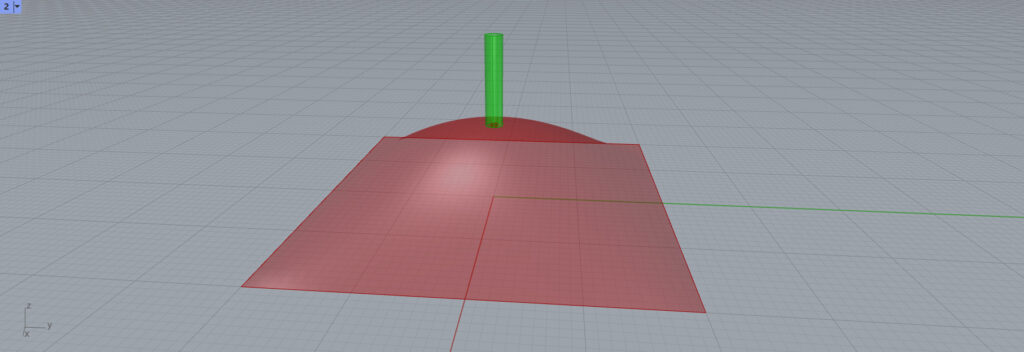
このように、円柱が作成されます。

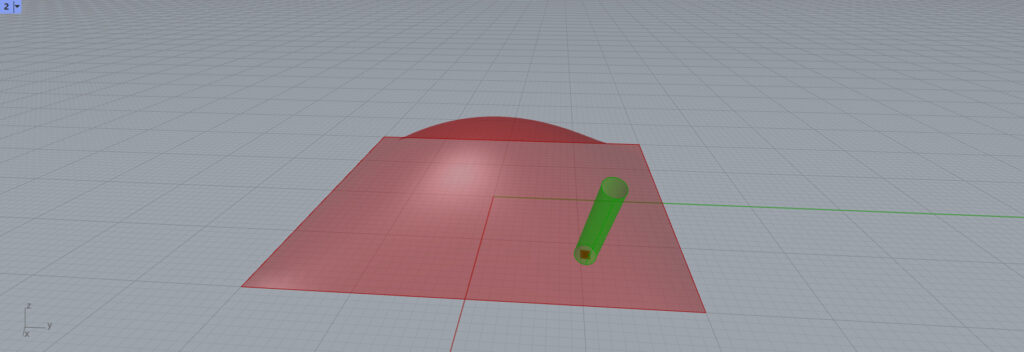
作業平面は、法線ベクトルとUVベクトルの情報をすでに持っているので、Cylinderのようなベクトルを指定する必要がないコンポーネントを使いうことができます。

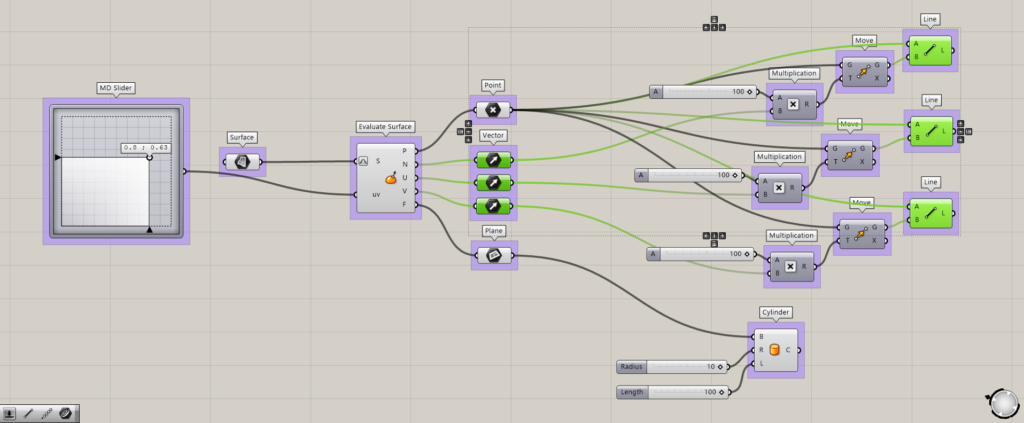
3つのベクトルを見てみます。

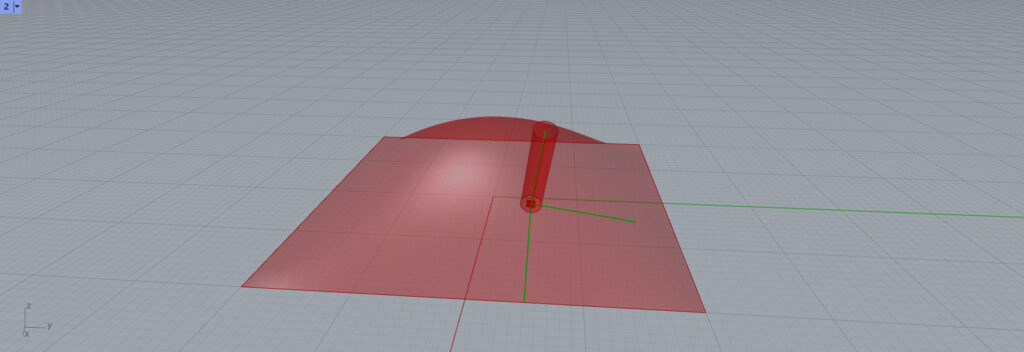
すると、円柱の位置に3つの線が見えます。

これで、作業平面は3つベクトルからなることが分かります。

Evaluate Surfaceコンポーネントを使用しているグラスホッパー記事はこちら↓